How many 3-clubs can a graph have?

A K-club on a graph is a subset of the vertices such that the diameter of the induced subgraph is less than or equal to K. "Induced subgraph" just means "pick all the edges which both endpoints in the graph."

I was answering this rather confused question over at Quora: https://www.quora.com/What-is-a-k-club-of-a-specified-graph-given-k-club-is-a-substructure-with-the-diameter-k-If-I-have-a-graph-with-ten-nodes-how-many-3-clubs-should-be-there/answer/Mark-Gritter

In it I pointed out that a 10-node graph could have as few as 10 3-clubs or as many as 127. The latter is achieved by this complete graph, for which every induced subgraph is a 3-club (and in fact a 0-club or a 1-club.)

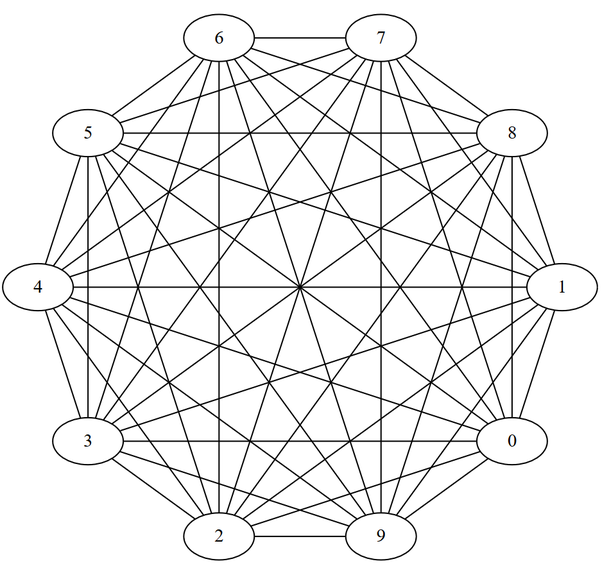
What about all of the intermediate values, though? Are there some numbers of 3-clubs that are impossible to attain?

I threw together some code to count all the possibilities, based on the enumeration of simple graphs here: http://users.cecs.anu.edu.au/~bdm/data/graphs.html

It looks, unsurprisingly, like all the intermediate numbers of 3-clubs are possible on at least one graph. Here's a stem-and-leaf plot for graphs of order 7. Every number between the minimum (7) and the maximum (127 = 2^7-1) is represented. That is, there is at least one graph that has N 3-clubs, for every possible N. The distribution shows some skew.

Number of 3-clubs
    | 789
  1 | 001122333444555666677777888899999
  2 | 000011112222233333444444555566666677788889999999999
  3 | 0000000111111122222333444444455555566667777778888888999999999
  4 | 00000111112222222333333334444444555555566666666667777777777778888889999999
  5 | 0000000000111111122222222233333333333334444444444444455555555566666666677777777888888888889999999999
  6 | 0000001111111111222222222222333333333344444444445555555555566666666666777777788888888889999999999999
  7 | 0000000000111111111111111112222222223333333333333344444444444455555555555666666666667777777777777778888888888888888889999999999999
  8 | 00000000000111111111111111112222222222222233333333333333344444444444455555555555555566666666666666677777777777777778888888888999999999999999999999
  9 | 00000000000111111111111122222222222222223333333333333334444444444444445555555555555666666666667777777777788888888888888888999999999999
 10 | 00000000000111111111111122222222222222223333333333344444444444455555555555555666666666666666677777777778888888889999999999
 11 | 00000000011111111112222222333333333444444445555556666666667777778888899999
 12 | 0001112223344567

I posted my code here https://gist.github.com/mgritter/0931cdd8e84da1eb91861411fab17d4e but unfortunately you won't be able to run it because:

• the enumeration of simple graphs at the link above is in a strange compact ASCII-only format
• which I did not parse
• but I did modify the source code of the provided parsing tool to make it not split edge lists across lines

I'll think if there's a way to visualize the results in a better way, but the results do not seem interesting enough to be worth pursuing (doing the count for 10-node graphs would take quite a while.)