Hi Steemians. Most of you probably had this classmate in high-school which tried to convince you that 1 is not equal to 1. The "proof" usually takes the form
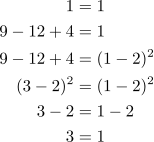
This is completely incorrect because
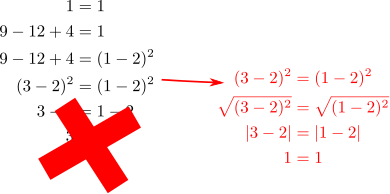
There is a bit of variety in these types of proof but they are all a bit silly.
But I upgraded this proof using some other fake proof methods (see the How did I create this "proof"?- section below) to a version which does not require any algebra! You just have to draw some pictures and you can convince somebody that 3=1!
A geometric "proof" that 3=1
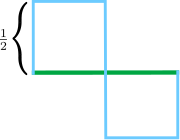
We start with a green line of length one:

The idea will be to approximate this green line by a line which has length 3. We will do this in a series of steps. First, we are going to draw the following Baby Blue line:
I will call this Baby Blue line BB (which henceforth you should pronounce as Bèbè because it sounds
 ). Each of the edges of BB are length 1/2. BB has 6 straight edges so BB has a total length of 6/2=3.
). Each of the edges of BB are length 1/2. BB has 6 straight edges so BB has a total length of 6/2=3.
This BB does not approximate the green line very well. I will scale BB by a factor 1/2 . Let us lazily denote the resulting line by BB/2. Then I can cover the green line with two BB/2:

The edges of BB/2 are length 1/4. Two BB/2 have 12 straight edges so in total it has length 12/4=3 which is again the same length as BB.
To approximate the green line even better I am going to scale BB by factor 1/3. The resulting line will be denoted by BB/3. Then I can cover the green line with three BB/3:

The edges of BB/3 are length 1/6. Three BB/3 have 18 straight edges so in total it has length 18/6=3. So we again get the same length as BB.
To get an even better approximation we can scale BB by a factor 1/n. The resulting line will be denoted by BB/n. Then I can cover the green line with with n pieces of BB/n. A single edge of BB/n is length 1/(2n). Observe that n pieces of BB/n consist out of 6n straight edges. So the total length is 6n/2n=3. Which means that the total length is always 3. In case you don't believe this I have drawn n=4,5,6 below:

If you look in the above figure then the baby blue curve is approximating the green line better and better. But if I let n go to infinity then BB/n will approximate the green line. The green line has length 1 and the total length of n pieces of BB/n is always 3. But then 3 = 1.
Where did we go wrong?!
There is a perfectly fine reason why you cannot conclude that 1 is 3. Mathematics did not just break. But I hope you can find the reason by yourself ;). Leave a reply below if you think you have found the answer.
Hint: Collect all the horizonal and vertical lines separately.
How did I create this "proof"?
This post is based on the famous pi =4 "proof" which I first encountered through a lovely Vi Hart video (click here). In her video she also gives a "proof" that square root 2 is equal to 2 which she then extends to a "proof" that a line of length 4 is equal to two times square root 2. The difference between my method and her method is that she uses a zigzag curve on the line . This zigzag curve requires some preperation to introduce so I think my version is a bit more elegant. Vi Hart does not really explain why the method yields an incorrect proof. However, Vi Hart seems to suggest a reason but it is incorrect (as you will hopefully also find out!).
Source
Figures made with inkscape. All the equations written using a phyton latex extension for inkscape. Both are free-ware!
Update
I actually wanted to do a post on a fun model/program I made for spreading infectious diseases but I found out in the weekend that even as a simple model it is really really really bad. On Monday I had the idea for this post. It took me a few nights to make this idea concrete so I don't have time for a second math post this week. Hopefully, I can create a math story about an infectious disease model by next week.
Thank you
Thanks for being so kind to read my post. You are awesome! Please follow me if you enjoyed it. If you have any questions just post them below and I will answer them. Or if you might have a nice topic you want me to cover also let me know below. :o)

Being A SteemStem Member
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well mathowl, don't you know that pi = 4
I mean look at the proof:
I am dropping a link to stackexchange and not taking the photo though you may have seen it before... Yes I know it is flawed
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yup I know that one. In the post I also refer to a video which presents the pi=4 "proof". :o)
The link you gave also does not pinpoint the problem :P
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
No it doesn't, however I have seen the proper solution (which points out the problem) a few times.
However the page has a few more problems, like the ones you discuss, which is why the link is a little better than just dropping an image.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
So far I have only seen the wrong reason. Although this is a nice video
The explanation is incomplete.
The suggested reason in this video is also incomplete (she is not very clear in saying if she is anwering the question or not)
I am pretty sure somebody out there must have a written nice explanation for it. But it most likely drowned in incorrect/incomplete answers
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
If you are so certain that there isn't an easy to find solution as to why this is wrong on the internet, wouldn't it be nice to add a follow up if no one in the comments gets the right reason? I'm sure you'll be able to provide the real, complete reason this doesn't work out.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
yes of course :o) but first think about it yourself.
I just realized that the hint I gave is not good. I changed it to: Collect all the horizonal and vertical lines separately. Now it is much clearer.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I'm assuming that it has something to do with the fact that the unit line is one dimensional, as in, it has no "thickness", whilst the baby blue line is two dimensional and sort of covers an area. So even though it looks to us like the line is approximating the unit line, the approximation is always off by still having "thickness". But I'm not versed well enough in maths to concretely describe my thoughts on this. I don't even know if my idea is going in the right direction at all or if it's much simpler than that.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yeah you are on the right track. The blue line has two directions. Take the sum of the length in each direction separately.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well, the sum of the length in the horizontal direction needs to be 1, otherwise the whole thing wouldn't make sense. Leaving us with a vertical length of 2. I am not sure how this helps me though.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
If you look back at the picture with the green and blue line. Imagine n goes to infinity are there still vertical lines left?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Of course there are, they are just infinitesimally small. Their sum doesn't change, it's still two.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My previous question was poorly phrased.
The blue line converges to the green line. But the green line has no length in the vertical direction. So where did all the vertical lines go?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I miss being in a college where we are proving this kind of numbers..@mathowl
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Math will never let you get something for nothing!!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
As usual, very nice article. I do appreciate that there are many who enjoy math in this way and I urge you to continue stirring the curiosity of steemit! :D Cheers!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit