Thought it would be fun to write a post about properties of (whole positive) numbers a.k.a. natural numbers. Hope you won't 8 it .

Number theory is a branch of mathematics which concerns the study of (surprise surpirse) numbers. More specifically, it concerns whole number. A great part of number theory involves selecting numbers through an interesting/beautiful/useful property and then showing that these selected numbers satisfy even more interesting/beautiful/useful properties.
Let's have a look at some cool numbers:
Narcissistic numbers or Munchausen numbers (named after the German baron with over-the-top adventures) are whole numbers which are equal to the sum of all its digits raised by the corresponding digit. So for example, since 1=11 it is a Narcissistic number and 3435=33+44+33+55 is also a Narcissistic number. There are only finitely many Narcissistic numbers in our base 10 counting system (=counting with 10 fingers). More generally, it turns out that in any base there are finitely many Narcissistic numbers[1]. I think that that is a pretty neat property.
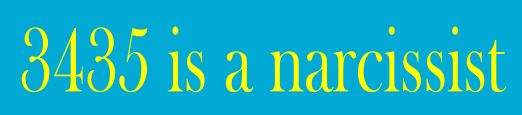
Friedman numbers are whole numbers which can be expressed as some combination of its own digits with any of the operations +, −, ×, ÷ (note that you are only allowed to use each digit once but you can use an operation as many times as you want). So 25=52 is a Friedman number. With some basic math you can show that it is the smallest Friedman number. You are also allowed to take two digits and turn them into a number, so 126=21 x 6 is also Friedman number.
There are all kinds of cool subsets of Friedman numbers. An exceptionally nice one are nice Friedman numbers which are numbers which preserve the order of the digits, so 343=(3+4)3 is a nice Friedman number because on the left hand side there first is a 3 then a 4 and finally again a 3. There are infinitely many Friedman numbers [2]. The remarkable thing is that if you consider a random number of n digits then the probability that this is a Friedman number converges to one if you let n go to infinity [2]. So there are many of these fellows if you consider numbers with sufficiently many digits. Unfortunately, this result remains unproven for nice Friedman numbers in base 10. But you can prove in certain lower bases which is nice [3].
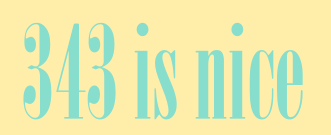
Perfect numbers are one my favorite numbers. So a perfect number is a whole number which is equal to the sum of all its divisors while excluding the number itself. For example 6 is a perfect number since its divisor other than 6 are given by 1,2,3 and 1+2+3=6. It is a simple exercise to show that 28 is also perfect number. There are many open problems related to perfect numbers. As computer power has improved we have been able to always construct a new largest perfect number [4]. That raises the question are there infinitely many? This is an open problem. If you take a look at a list of perfect numbers you notice that they are all even [4]. Can we prove this? No, this is also an open problem. However you can prove that perfect numbers are connected to a special type of prime number, called Mersenne primes [5] (check out this Numberphile video for an easy to understand proof). Which is awesome.
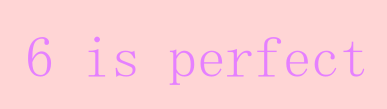
Are all numbers interesting?
I could go on all day talking/writing about numbers but this might lead you to asking the question: do I think that all (whole) numbers are interesting? And the answer is yes. Let me prove it to you. Suppose there exists a (non-empty) collection of numbers which are uninteresting. Then there must exist least interesting numbers which is an interesting property. So there you have it: all numbers are interesting :D
This is paradoxical statement is also known as the interesting number paradox [6]. (I actually have no idea who came up with it so if you know where it originally came from let me know in the comments below). Since I am proven to be interested in all numbers tell me your favorite number in the comments below :D
References
[1] D. van Berkel, On a curious property of 3435. https://arxiv.org/pdf/0911.3038v2.pdf
[2] M. Brand, Friedman numbers have density 1, Discrete Applied Mathematics, 161(16–17), Nov. 2013, pp. 2389-2395.
[3] M. Brand, On the Density of Nice Friedmans, Oct 2013, https://arxiv.org/abs/1310.2390
[4] M. Pedersen, A list of known perfect numbers https://web.archive.org/web/20090503154707/http://amicable.homepage.dk/perfect.htm
[5] L. Euler (1849), De numeris amicibilibus, Commentationes arithmeticae (in Latin), 2, pp. 627–636. Originally read to the Berlin Academy on February 23, 1747, and published posthumously. See in particular section 8, p. 88.
[6] B. Brunch, Mathematical Fallacies and Paradoxes, New York 1982.
Remark concerning [1]: The number of Narcissistic numbers actually depends on if you assume that 00=1. If you assume this then for base 10 there exist 4 Narcissistic numbers 0,1, 3435, and 438579088. This paper does not assume that 00=1 so it says there are only 2 Narcissistic numbers for base 10.
All images made with inkscape. It is free!
Merchandise :D

There is a MathOwl shop which sells my artsy fartsy stuff. If you got some spare money head over there. You can learn about the colors of pi over here here. I also have really cheap stuff available like these stickers They are an absolute hoot.
Join #steemSTEM
#steemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics related content and activities on the STEEM blockchain. If you wish to support the #steemSTEM project you can: Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Join our Discord community | Delegate SP to steemstem
Convenient Delegation Links:
For math 9 is my favorite number. I like that when you add it to a number the sum is plus ten less one of that number. That when you multiply a single whole number by 9 the sum adds up to 9. There are many cool things about a 9 in math.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
9 x 9 = 81 = (8+1)x(8+1) :D yeah that is a cool property.
I think it only works below a certain number. Probably the general rule is that the sum is divisble by 9. For example 9 x 12345678901 = 111111110109. If you take the sum of the digits it is greater than 9. The sum is divisible by 9 :D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
What I was talking about is 9x9=81 8+1=9, 9x8=72 7+2=9, all the way to 9x1=9 + 9=18 1+8=9
I use fuzzy math when I add being a carpenter it makes me be able to figure up cut list quickly without using paper.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yeah I got it. That trick works when the n in n x 9 is a whole number less or equal to 10. For n is greater than 10 it does not necessarily work. For example, when n=11 it fails since 11 x 9= 99 and 9 + 9 =18. So then the question is what kind of property do the sum of digits satisfy when we consider all n? Well, apparently you can prove that the sum of the digits is always divisible by 9. So in the case of 11 x 9 = 99 since 9 + 9 =18 it is easy to see that it is divisble by 9. Now let's try 12 x 9 =108 so 1+0 + 8 =9 so that is definitely divisble by 9, for 12345678901 x 9 = 111111110109 we have that 1+1+1+1+1+1+1+1+0+1+0+9=18 and that is divisble by 9 :D
(I thought that -> 9 x 9 = 81 = (8+1)x(8+1) was just a nice way of writing this property. Since everything is one equation. It also works for the others for example 9 x 8 = 72 = (7+2)x(7+2) :D )
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My favorite number is 11. A few years ago, every time I checked the hour, it had 11 minutes in it. But I know that was my subconscious making me check the hour in those moments, because something similar happened to me with 3:33AM, there was a time when I automatically started to wake up at that hour. Both cases after reading weird things about those numbers. After a while it stopped.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thats too early! :D 3:33am what were u waking up to do really, is it to pee?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
No haha not to pee, I don't know why, I just use to wake up, check the time, and back to sleep.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
11 is cool. But generally numbers with just one in them have some cool properties. For example:
1x1=1
11x11=121
111x111=12321
etc
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I wonder if it is correct?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Big bang theory? :P
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Exactly. Hahaha.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My faavorite number is 7:" its a very special and unique number just like 9.
Very interesting article mathowl
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Those are nice numbers what do you like about them? :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well , I like them for liking sake, and I think its because I was born on the 7th month.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by mathowl from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My favorite number is 47. It should be obvious why :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
yes its obvious. You are 47 year old :P
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
:(
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
seriously I don't believe this. I was joking :(
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You like guns?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
And suits!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
So you are an agent :o)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Who knows? :O
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
your age?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
My favourite : 7
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
What do you like about 7?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sadly for no reason this number got stuck in my mind from childhood days. Maybe because of 7 musical notes, 7 colors thing. 7 has a mythical charm for some reason. No specific explanation
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @mathowl!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
i always thought 7 is the perfect number. Mythical? Maybe, now i know the facts. Personally i don't have a favorite number. But its good to know some numbers are nice, perfect or narcissist.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit