The math of connecting galaxies in an efficient way

Hi Steemians, I wrote another math story. This time about outer space. It is a bit of a hairy story even though there is no' air in space :D

It is the year is 3019 and intergalactic space travel is possible. It works by building special space roads between galaxies. Building of these roads is controlled by the council of Intergalactic space travel which hires special contractors to build these roads. For the CX15-alpha sector the council hired the Pioneering Roadworks for Intergalactic Movement company, or PRIM for short. Their CEO Bob had landed this contract by undercutting all the competition.

Just to show you what the CX15-alpha sector looks like here is a picture of the subsystem B1 of the CX15-alpha sector:

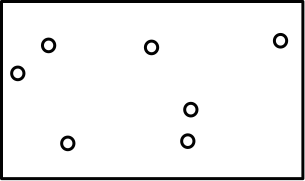
Every tiny circle represents a galaxy. The distances between each galaxies on this map correpond to the real distances times a scale factor.

Back to Bob the CEO

When Bob arrived back in his office he opened a nice cold beer and went to check on his computer wheter the council already had transferred the funds. "A good they have already transferred it. Well let me just check if the numbers are ok", said Bob to himself. Bob looked and froze. It was only one tenth of the suggested amount. "Well....that must be mistake", thought Bob. He pulled out the contract from his briefcase and looked at the numbers. Bob's face turned instantly white. The number on the contract was the same as the money transferred by the council. Bob realized that he had forgotten a zero when he wrote the contract. Dazed by his mistake he just blankly starred ahead.

Time for a new plan

It took a good 10 minutes before his brain rebooted. His eye fell on the intergalactic roadworks plan for the B1 subsystem:

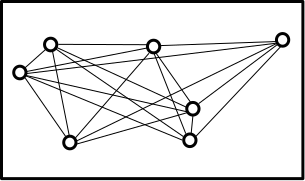
The blacklines are the intergalactic roads. As you can see every galaxy is connected to every galaxy. Travel along these roads to the connecting galaxy only takes a few minutes.

Bob suddenly realized that since travel along these roads is so quick he didn't need to directly connect all galaxies in this subsystem. For example, instead of using three roads to connect the following three galaxies:

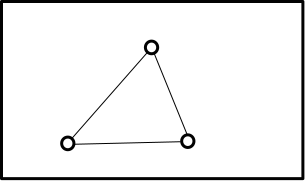
Bob actually only needs to construct two roads:

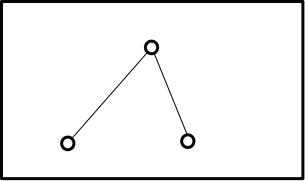
As you can see there is a path connecting all the galaxies which consists out of two roads.

Of course the longer the path the more expensive it is to build it. So the question that Bob asked himself is:

What is the minimal length of intergalactic road that is needed to create a path connecting all galaxies to each other?

Bob's method

"Hmmm, so how should I do this? " thought Bob. If you don't know what to do then you better start with what you should not do. It was clear to Bob that his road network should not contain any loops. Since if it contains a loop then you can always remove one intergalactic connection. This gives Bob the following rule:

RULE: never make any loops

But how can you find a path without loops which is minimal. Where should you start looking for a minimal path? Since there should exist a path connecting all galaxies you can start anywhere. I colored the galaxy where Bob starts red:

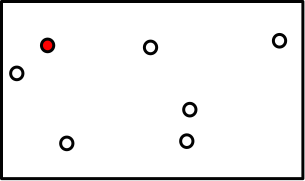
Where should the first road be? Since Bob wants to build the shortest possible road he adds the road to the nearest galaxy:

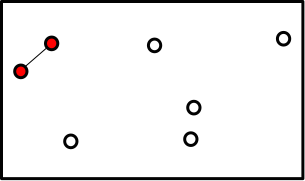
The galaxies which are connected are now colored in red. Bob can then continue by adding the shortest possible road connecting one of the red colored galaxies to the white colored galaxies:

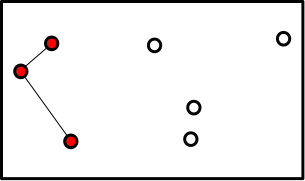
The galaxies which are connected have been colored in red. Bob repeats this process by again adding the a road to the nearest galaxy which connect the red colored galaxies to the white colored galaxies. However, he needs to keep in mind his RULE to never make loops:

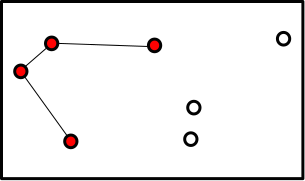
Bob then repeates this process until he has connected all the galaxies:

Bob isn't sure if this is minimal so he wants to start from a different galaxy and repeat the whole procedure:

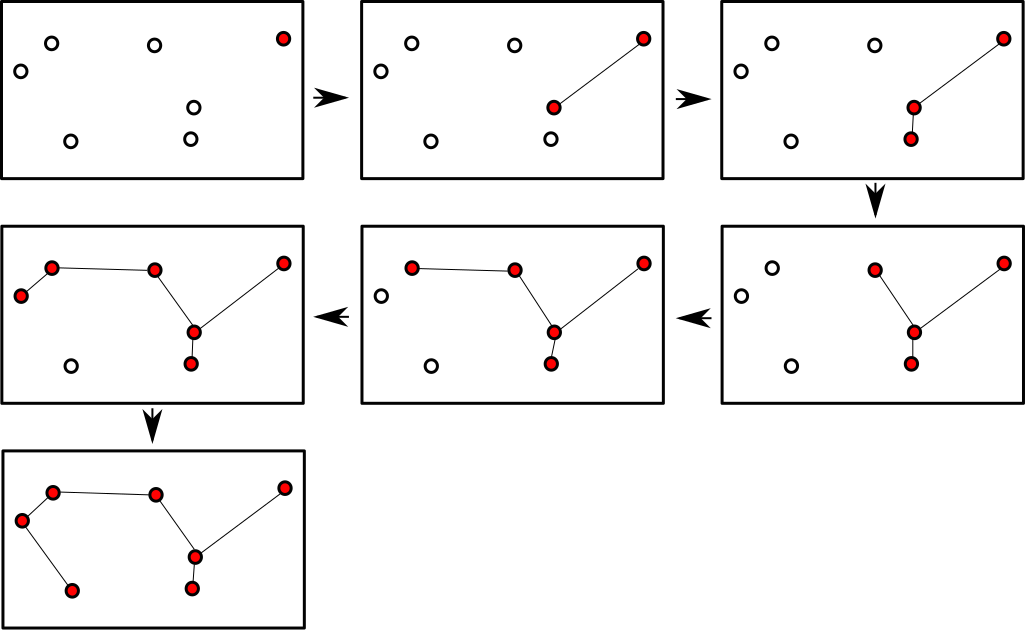
He ends up with the roads! Bob quickly realizes that because he constructs the total path by always adding the shortest road it does not matter where he starts. Or formulated differently:

It is minimal because Bob always adds the shortest road.

(note: this is not 100% true, for details check the technical appendix below).

Bob is amazed by this result. "Well I better patent this method." says Bob. "My company is called Pioneering Roadworks for Intergalactic Movement so I better name this method PRIM's method!"

---

Background and conclusion

Unfortunately for Bob this method has already been invented. It actually has been several times reinvented. First one to discover it was Vojtěch Jarník. It was later rediscovered by Robert Prim as well as by Edsger Dijkstra. This method is usually referred to as Prim's algorithm (surprise!) or Dijkstra's algorithm. But I found out from wikipedia that apparently nowadays they also call it the DJP (Dijkstra-Jarnik-Prim) algorithm Wiki.

Prim's algorithm is as greedy as possible at each step since it selects the nearest galaxy to build a road to. Algorithms which are greedy at each step are referred to as greedy algorithm. Not all problems can be solved using greedy techniques. This is because of the simple reason that the best choice at a single step is not always the best choice over all the steps. Or formulated differently, what locally/short-term is the best is not always the best globally/long-term. For example, if you eat all your snacks for the week on the first day of the week you might be very happy on the first dat but most likely you will have a bad time for the rest of the week. So the quote

Greed is good. -Gordon Gekko (1987)

Should actually be

Locally/short-term greed is good, globally/long-term might be good. - Mathowl

---

Technical Appendix

The statement It is minimal because Bob always adds the shortest road is incomplete. This has to do with the RULE. So at each step of Prim's algorithm you need to make sure there are no loops. Theoretically, there might be a step where the adding the shortest road will create a loop. It requires a tiny but technical proof to show that this situation can never occur. On the second page of these algorithm lecture note by Dinitz you can find the full proof.

---

---

Sources and further reading

For a more detailed description of Prim's algorithm you can head over to the Wiki. These type of algorithms belong to the field of discrete optimization. If you have a bit of a mathematical background you can learn more about discrete opimization in these lecture notes by Schafer.

Top picture by Genty from the pixabay.

The figures (including the banner below) were made using Inkscape

Owl tax

Photo by Kdsphotos - Pixabay

---

Join #steemSTEM

If you want to know more come and join us at discord: https://discord.gg/BZXkmWw


CC0 creative commons made by Mathowl, feel free to use this banner :)

Shoutout to @anevolvedmonkey for spotting that I made a mistake in the banner with my perfect numbers. It has been corrected.