The numbers exist independently of their representation. However in order to use them, in everyday life, in science and in "pure mathematics", we need to represent them in some logical way. Along history, civilizations have used different ways and methods to represent the numbers in order to manipulate them. This is done by the systems of numeration or numeral systems.
Now days, we use the decimal system or system base 10, as it is also called. For example what does the representation of the number "2017" mean? The answer is
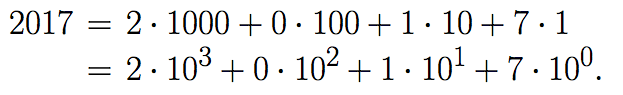
In general the integer number dn... d1d0, in base 10 means
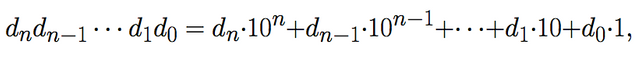
where the digits di's are numbers between 0 and 9.
We can represent the numbers in other bases, and some of them are widely used in technology. For example the computer science the binary system (base 2) and hexadecimal system (base 16) are extensively used.
In the binary system, only two digits are used 0 and 1. So the expression bn...b1b0, where the bi's are 0 or 1, is the number given by
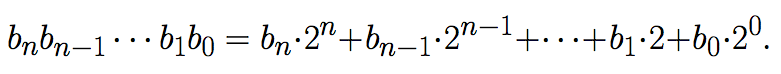
For example the number 11001 in binary is
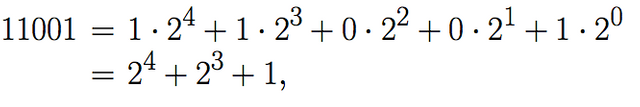
which corresponds to the number 25 in the decimal system, since
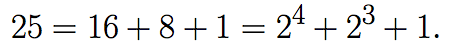
In order to avoid confusion, when the number bn...b1b0 corresponds to the binary expression, usually is denoted in the following way (bn...b1b0)2 , where the subindex 2 means the binary expression of the number. So in the previous example 25=(11001)2.
In general for any number p, we can write
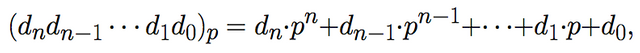
where the digits di, are numbers between 0 and p-1.
For example
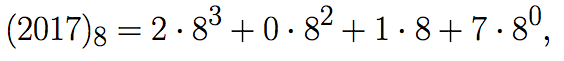
which corresponds to the number to the number 1039 in the decimal system since
1039=2⋅83+8+7.
In computer science the hexadecimal system is broadly used, here p=16, so 15 digits are needed. For this reason some letters are incorporated as digits. The following digits are commonly used:
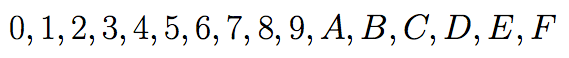
They represent the values of 0 to 15 respectively. For example:
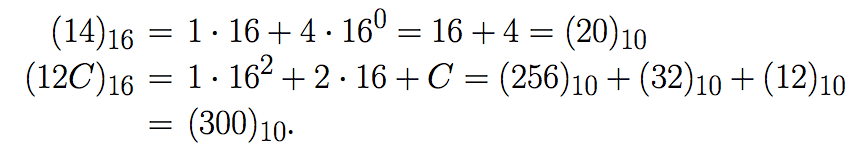
In other words (14)16 and (12C)16 are the hexadecimal representations of the decimal expressions 20 and 300, respectively.
In different branches of mathematics, base 3 is sometimes used.
Why do we used base 10? This is mainly because we have 10 fingers in our hands and used them for counting. It is worth mentioning, the word "digit" comes from the latin digitus that means "finger" or "toe".
The binary system is used mainly in computer science because adding numbers is very fast and efficient by the electronic circuits.
As it can be observed the larger the base p, we need to have more digits and it could be cumbersome to handle the representations, on the other hand if the base is too small, like two, small numbers have very long expressions and are difficult to handle for everyday usage.
The Babylonian civilization used the sexagesimal numeration system (or base 60). The main advantage for using this numeration system is because the number 60 has 12 different factors ( 1,2,3,4,5,6,10,12,15,20,30,60 ), which facilitates many computations. The Greeks also used the sexagesimal system in astronomy. Now days, we still use this system in how we measure angles and time.
The representation of numbers in the numeral systems that I described here are called positional representation, clearly the way how the romans denoted the numbers are not based on the position and they not used digits. Doing arithmetical computations in the roman system is very cumbersome.
So far we have discussed the representation of integer numbers. In the following lines, we explain the representation for non-integer numbers.
For example the decimal expression 21.1023 is
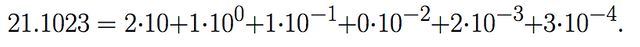
In general the expression (dn...d0.f1f2....)p means
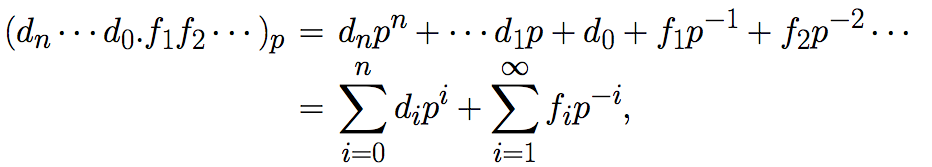
where the digits di and fi are numbers between 0 and p-1.
The number (dn...d0.f1f2....)p is rational if and only if the expression terminates or is repeating, i.e. after some k all the digits fk are zero or they repeat in a periodical manner.
The rationality of a number is independent of the base used.
However the expression of a number could repeat in a base and terminates in other base. For example:
1/3 in the decimal system is 0.3333.... repeating infinitely many 3 and in base 3 is (0.1)3.
We have to remark that the expressions including fractional part (non-integer) numbers might not be unique. For example in the decimal system 0.9999999..... is equal to 1, since
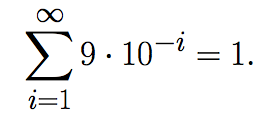
The expression of any irrational number is not periodic nor terminates in any base.
Consider the number π, in the following lines can be seen its expression in different bases:

The ancient Greek astronomer Ptolemy, knew the following approximation of π in base 60:
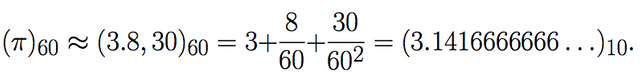
References:
https://en.wikipedia.org/wiki/Hexadecimal
https://en.wikipedia.org/wiki/Sexagesimal
https://en.wikipedia.org/wiki/Numeral_system
Hay algo interesante sobre los números irracionales, por ejemplo Roger Penrose en su libro El camino a la realidad , dice que la introducción de los números complejos es más sencilla que la de los irracionales, no recuerdo sus argumentos y explicaciones al respecto, pero sin duda es interesante ya que, a excepción de los números irracionales, los números complejos se ven apenas en quinto año, y no siempre.
Gracias por tu publicación
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Los números reales son complicados, no se entendieron bien hasta el siglo XIX. Los griegos introdujeron la idea que cada punto de la recta (real) corresponde a un número real. Se dieron cuenta de la existencia de los irracionales. Sin embargo la introducción de los reales en análisis, es más sofisticada. Una propiedad fundamental de los números reales es la del supremo ( e ínfimo). Hay tres maneras de introducir los reales: Una axiomática, o bien construyéndolos como clases de equivalencia de sucesiones de Cauchy de números racionales o la construcción basada en cortaduras de Dedekind. Los números reales es un objeto matemático bastante sofisticado.
Los números π y e, no son solo irracionales sino trascendentes. Se conocen pocos números trascendentes, a pesar de que su cardinalidad es no numerable.
Gracias por el comentario.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I studied some bit of numerology during my physics undergrad, but never really considered what Pi would look like in any other number system outside of base 10.
Thanks for the brain-stretcher!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit