This is a continuation of my last post An introduction to algorithmic information theory PART 1
In the last article we asked whether we could prove that incompressible bitstrings exist. With incompressible we mean a bitstring whose Kolmogorov complexity is not much shorter than its length. The Kolmogorov complexity, or the algorithmic complexity, is defined as the length of a shortest program, p, that writes out the bitstring, x, and then halts:
K(x) = min {l(p): U(p)=x}
Let's assume that M is the set of all bitstrings of length n:
M = {x: l(x)=n}
How many of these strings can be compressed by no more than c bits? Hence we want to estimate how many of these strings satisfy: K(x)>=l(x)-c. We can estimate this with a simple counting argument; there simply aren't enough programs with short lengths, hence there cannot be that many strings, x, with low complexity. Here |A| denotes the number of elements in A. Let's denote this by:
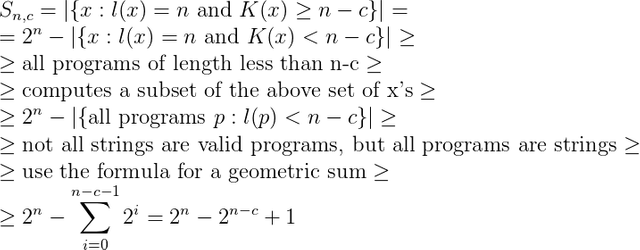
We see that at least (c=0) one string of length n cannot be compressed at all: K(x)>=n. At least half of the strings plus one cannot be compressed more than one bit. At least 75% of the strings plus one cannot be compressed more than two bits and so on. Basically a very small amount of strings can be compressed many bits, so most of them are not substantially compressible.
Let us now estimate the corresponding number for the number of strings shorter than or equal to N:
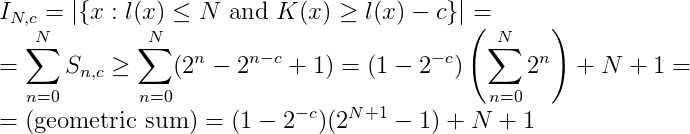
Let us compute the proportion of strings with length <=N that cannot be compressed more than c bits. First, the total number of strings with length <=N is:
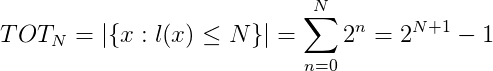
Therefore the proportion of strings with lengths <=N that can be compressed no more than c bits is:
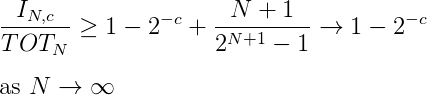
We see that as N goes to infinity, i.e. the above set converges to the set of all strings, then the proportion of all strings that cannot be compressed more than c bits is at least 1-2^(-c). Hence almost all strings, is not compressible by many bits.
Please don't miss my next post and don't forget to upvote, follow and resteem.

This post received a 2% upvote from @randowhale thanks to @rndness222! For more information, click here!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit