Let S be the set of all functions f such that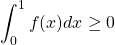 
. Assume that S is a real linear space. Then, by the addition axioms of real linear spaces, there must exist an element g in S such that f + g = 0. We will show that this leads t a contradiction, thus proving S cannot be a real linear space.
Assume f is in S, and has the additive inverse (axiom 6) g such that f + g = 0. Then the primitive of f, F(x) satisfies the property:
F(1) - F(0) ≥ 0.
This implies that F(1) ≥ F(0), so f(x) must be greater than zero, since f(x) is the derivative of F(x), and F(x) must be increasing.
At the very least, (f(1) + f(0))/2 ≥ 0 (the average slope of the primitive must be positive or zero)
But this must also hold true for g and its primitive G, since g is also an element of S. But if f ≥ 0 and g ≥ 0, then (f + g) ≥ 0. The only (f + g) = 0 is if f and g are both zero, since neither can be less than zero.
But S allows for all functions such that .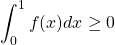
Thus, there cannot exist a negative element g for every element f in S for 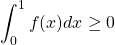. Only those functions f that are equal to zero can have a negative element. Therefore, S cannot be a real linear space.
QED
@OriginalWorks
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit