Let S be the set of all vectors v such that v = < x , y, z > with 3x + 4y = 1 and z = 0. Then, x =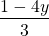 
and y = 
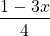. So, v = <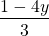, , 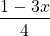0>
Proof:
Assume S is a real linear space, then S must be closed under addition (axiom 1). In other words, if v and w are in S, v+w must also be in S. By that logic, if v is in S, v + v = 2v must also be in S. Another way of saying this is that S must be closed under scalar multiplication (axiom 2).
But for all v in S, v must equal <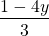, , 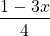0>
Yet multiplying v by any constant c, breaks that form. So S cannot possibly be closed under scalar multiplication or addition.
Therefore, S cannot be a real linear space.
QED
@OriginalWorks
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit