Hello steemit readers!!
Welcome to the second chapter of this series on a gentle introduction to mathematics. In the previous posts, we were able to cover so many basic concepts in mathematics that now we are equipped to move higher in mathematical abstractions.
First, we've encountered basic sets, we were also acquainted with some properties of prime numbers, and we delved into more scary notations as we gained more familiarity with the lexicons of mathematics. We were also introduced to some basic concepts in elementary number theory, some important algorithms in elementary number theory and we saw the power of relational symbols.
Today, we are going deeper into the field of logic. In the prime numbers, we emphasize the importance of establishing a precise definition of terms. Here's an interesting fact:
In every branch of mathematics, there are some atomic, notions that defy precise definition.
In the field of geometry, for example, the atomic notions are points, lines, and their incidence. According to Euclid, a point is “that which has no part”. That’s where things get confusing because, in real life, we denote a point as a dot, which has parts intuitively. Does this imply that anything without volume, area or length is a point?
That truth is mathematicians have recognized that a formal argumentation has to have such elemental, undefined, concepts. In Euclid’s geometry, the notion of “point” can’t really be defined.
In the field of set theory, the atomic concepts are “set”, “element”, and “membership”. While in logic, the atomic concepts are “true”,“false”, “sentence” and “statement”.
On the concept of “true” and “false”, I hope there is no uncertainty regarding their meanings.
A sentence is defined to have a well-understood meaning that most will agree on – a syntactically correct ordered collection of words such as:
a. “Steem is a blockchain-based rewards platform for publishers to monetize content and grow a community."
b. “Bitcoin is a cryptocurrency.”
c. “John is on steemit.”A statement is a sentence whose truth value is definite. In simple words, a statement can be decided to be either true or false.
The first two example sentences are agreeable. The third one is ambiguous unless we know who John is.
Ambiguity is one reason why a sentence may not be a statement. Note however, that as we encounter more complex statements, it may be the case that the truth value of a given statement simply cannot be decided.
Kurt Godel’s “Incompleteness Theorem”
Godel’s incompleteness theorem's important aspect is the proof that in any mathematical system, there must be undecidable sentences – statements which can neither be proved nor disproved from the axioms.
Predicate
Suppose I came up to you in a windowless room and make the statement: “The sun is shining but it’s raining!” You decide to investigate the veracity of my statements, and came up with four possible combinations of sunniness and/or precipitation.
Look at the table below were we have introduced a convention – T indicate a true statement, while Greek letter phi indicates a false statement.

truth table
Our atomic predicates are: “The sun is shining” and “It is raining”, which can be true or false independently of one another.
Each row in the table represents a possible state of the outside world (sunny and/or rainy). Assume that you observe the last condition, that is, it is neither shining nor raining. Then you can conclude that I am not to be trusted. My statement, the compounding of “the sun is shining” and “it is raining”, is false. A rewording of my statement can be stated as:
“The sun is shining but it is raining”
If you think about it a bit, you’ll agree that this so-called compound sentence is true only in the case that both of its component pieces are true. An amusing linguistic point about this is “but” and “and” have exactly the same meaning!!
More precisely, they denote the same thing.
Connectives
In mathematics, we distinguish two main connectives for “connecting” simple sentences into compound ones.
- Conjunction: the compound sentence is made by sticking the word “and” between them
- True only when both components are true
- Disjunction: the compound sentence is formed by placing an “or” between them
- False only when both components are false
One begins to suspect that mathematicians form an unusually lazy sub-species of humanity.
As always, mathematicians have developed an incredibly terse, compact notation for these ideas.
First, we represent an entire sentence by a single letter – conventionally using a capital letter. This is called a predicate variable. In our example, we could denote the sentence “The sun is shining” by the letter S. Similarly, we could make the assignment R = “it is raining”.
We can represent the statements of the compound sentences as:
- For conjunction:
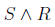
- For disjunction:
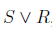
As a mnemonic, note that the connectives in the conjunction look like the capital A (as in “And”). The effect of these two connectives can be displayed in a truth table.
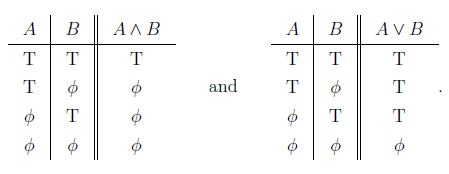
Conjunction and Disjunction Truth table
A truth table is a list of all possible truth values of the predicate variables and then enumeration of the truth values of some compound sentence.
In addition to these connectors we need a modifier – something that acts on a sentence and modifies it to its opposite meaning – we call it negation. It is also known as the denial of a sentence. We shall denote the negation of a sentence A as,
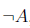
And its truth value is exactly the opposite of A’s truth value.
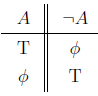
These three simple tools (and, or & not) are enough to create complex sentences out of basic components. The study of these logical operators is called Boolean Algebra.
Previous topics you may want to read:
- A Gentle Introduction to Mathematics - Basic sets
- A Gentle Introduction To Mathematics - Prime Numbers
- A Gentle Introduction To Mathematics - More Scary Notations
- A Gentle Introduction To Mathematics - Elementary Number Theory
- A Gentle Introduction To Mathematics - Algorithms
References
Thank you for reading ...


..Good Stuff! In digital electronics, all the logic functions are implemented using devices called logic gates which are made from transistors such as the AND gate, OR gate and NOT gate. A computer microprocessor does it's thinking by performing the logical functions given by the mathematics above....
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yeap, @akinkunmi, mathematics is the foundation of everything we have now, including as you said digital electronics. Not to mention, blockchain powered by cryptography (with underlying difficulty based on prime numbers factorization)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has received a 3.94% upvote from thanks to: @sinbad989.
thanks to: @sinbad989.
For more information, click here!!!!
Send minimum 0.050 SBD/STEEM to bid for votes.
Do you know, you can also earn daily passive income simply by delegating your Steem Power to @minnowhelper by clicking following links: 10SP, 100SP, 500SP, 1000SP or Another amount
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
i wish i could met you when i was a kid
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit