Now, we are done with the introduction chapter of the book, Elements of Set Theory. Again, I would like to emphasize the importance of the axiomatic method which we will employ throughout the book. And from this axioms, which begins with the primitive notion of "sets" and "numbers", we will define others.
In the second chapter we will be dealing with axioms and the possible operations you can do in the sets. In this chapter, we are going to introduce the first six of our ten axioms. It may seem at first to be a cumbersome machinery to use axiomatization, but it will eventually prove itself to be a powerful machinery for difficult tasks.
Axioms that will be introduced were not chosen at random, but it somehow reflect the informal ideas about what sets are.
So, let's get started.
Elements of Set Theory: Axioms
1.Extensionality axiom: If two sets have exactly the same members, then they are equal:
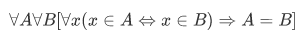
Next are axioms assuring the existence (note: $\exist$ in these axioms) of some basic sets that we've encountered informally in the preceding sections.
2.Empty set axiom: There is a set having no members:
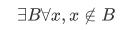
Definitions:
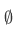is the set having no members.
Other set existence axioms justify the definition of the following symbols.
The set existence axioms (2) assure us that the empty set exist, and the extensionality (1) assures us that the sets being named are unique.
3.Pairing axiom: For any sets u and v, there is a set having as members just u and v.
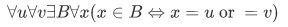
4.Union axiom (preliminary form): For any sets a and b. there is a set whose members are those sets belonging either to a or to b. (or both).
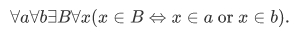
5.Power Set axiom: For any set a, there is a set whose members are exactly the subsets of a:
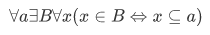
Definition:
(i) For any sets u and v, the pair set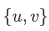 
is the set whose only members are u and v.
(ii) For any sets a and b, the union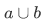 
is the set whose members are those sets belonging either to 
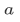or to 
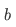(or both).
(iii) For any set 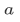, the power set 
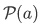is the set whose members are exactly the subsets of .
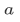We can use pairing and union together to form other finite sets. First we have to introduce the singleton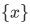 
given any 
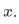This singleton is defined to be 
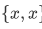. And given any 
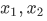and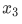 
we can define
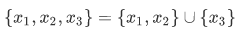
We have defined the union operation, we can then defined the intersection operation. But in order to introduce the intersection operation, we have to introduce a new axiom.
To formulate the new axioms, we have to use our informal view of sets. Note that our set existence axioms contain expressions like
"there is a set $B$ whose members are those sets
satisfying the condition _____"
If the axiom mention some other sets 
, then the full version becomes
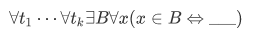
with the blank filled by some expression involving
, and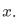 
.
The empty set can all be patterned in this form, rewritten as:
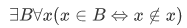
which is just equivalent to saying that the other sets
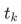is set at 
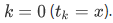. The set $B$ is uniquely determined by 
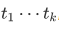, and has an existence asserted by the extensionality axiom.
Now let us be more general and consider any sentence $\sigma$ of the form
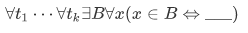
where the blank is filled by some expression involving at most
, and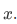 
If the sentence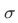 
is true, then the set 
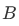could be named by using the abstraction notation:
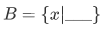
The sets we have encountered recently can be defined by the use of the abstraction notation:
6.Subset axioms: For each formula ___ not containing B, the following is an axiom:
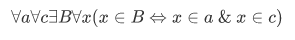
In this section we include the following axioms in this list:
- subset axioms, infinity axioms, choice axiom, replacement axioms, regularity axiom
Subset axioms
This axiom asserts the existence of a set $B$ whose members are exactly those sets x in c such that ___.
One of the subset axiom is the following:
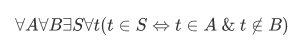
This axiom asserts the existence of the set we define to be the intersection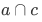 
of 
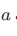and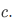 
.
We can also allow the following subset axiom:
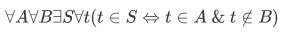
This set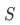 
is the relative complement of B in A, denoted 
.
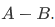Note on Terminology
The subset axioms are often known as Aussonderung axioms. The word Aussonderung is German, and is formed from sonderen (to separate) and aus (out).
In future chapters, we will construct the set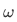 
of natural numbers:
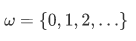
And using the subset axioms we can form the set of even numbers and prime numbers:
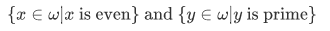
(but of course, we should express the "x is even" and "y is prime" in some legal formula; we'll return to this shortly).
Theorem 2A:
There is no set to which every set belongs.
Proof:
Let's assume we have set A and we will construct a set not belonging to A, that is,
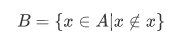
We claim that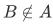
. By the construction of B, we have
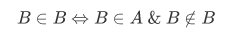
If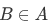 
then this reduces to
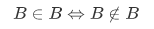
which is impossible (a paradox), since one side is true and the other is false. Hence,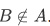 
.
One interesting fact that we shall say right now is that a set can never be a member of itself. (we will argue much later in Chapter 7).
At this point we need to know what a formula is. It saves us from writing long sentences and instead use logical symbols. By insisting that the formula be expressible in the formal language these symbols give us, we can eliminate "long wordy sentences".
Symbols will be our friends!
The logical symbols are: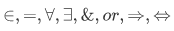 
Complicated formulas can be built up from these together with enough parentheses to avoid ambiguity.
We define a formula to be a string of symbols constructed from the simplest formulas by the use of the above-listed methods.
Example:
Let $s$ be some set. Then we formed the set of one-element subsets of s:
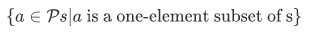
The "a is a one-element subset of s" is not a formula, but we can rewrite it as a formula. But first lets chop this into parts.
- First a must be a subset of s (of course):
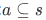
- The set a should not be a empty set: $
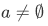
- Any two members of a must coincide:
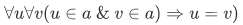
This in turn becomes the formula:
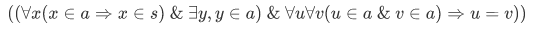
This example is generally an example as to why we will not write out the formula in the application of subset axioms. The sentence, "a is a one-element subset of s" is much easier to read than the legal formula.
But in every case it will be possible to eliminate the English words and the defined symbols in order to arrive at a legal formula.
Disclaimer: this is a summary of section 2.1 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora
