Consider the situation where I want you to guess the function such that I only give you two information; that is,
- a starting value
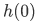
- a function
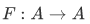 such that
such that 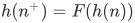 for all
for all 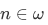
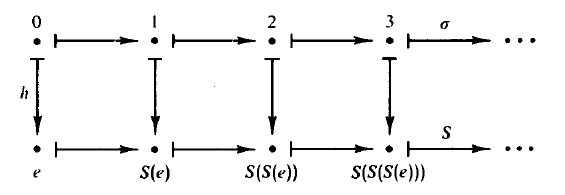
This gives away all the information where you can compute successively,
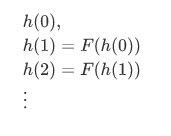
Now for a harder question: Suppose we are given a set A, an element 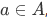 , and a function
, and a function 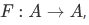 , then how can we show that there exists a function
, then how can we show that there exists a function 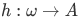 such that
such that
We can prove that there exists a set h that is a function meeting the above conditions.
Recursion Theorem on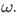 Let A be a set,
Let A be a set, 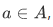 and
and 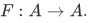 . Then there exists a unique function
. Then there exists a unique function 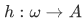 such that
such that
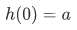
and for every
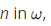
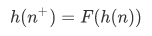
Proof
First, we will let h be the union of many approximating functions. For the purpose of this proof, call a function v acceptable iff  , and the following conditions hold:
, and the following conditions hold:
(i) If 
(ii) If 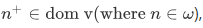 then also
then also 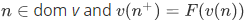
Let 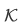 be the set of all acceptable functions and the union of this set is the h function:
be the set of all acceptable functions and the union of this set is the h function: 
We claim that this h meets the demands of the theorem, breaking it down into four parts.
- h is a function
- h is acceptable
- dom h is all of
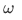
- h is unique
Example Let 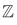 be the set of all integers, positive, negative, and zero:
be the set of all integers, positive, negative, and zero:
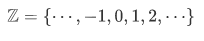
There is no function 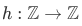 such that for every
such that for every 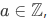 ,
,
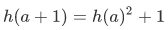
If you notice,
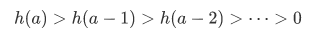
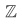 has no starting point similar to the 0 starting point of the recursion on
has no starting point similar to the 0 starting point of the recursion on 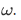 .
.
Our first application of the recursion theorem will be to show that any Peano system is "just like" 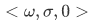 . There are other Peano systems; for example, let N be the set
. There are other Peano systems; for example, let N be the set 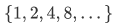 of powers of 2, let
of powers of 2, let 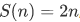 , and let
, and let 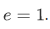 . Then
. Then 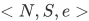 is a Peano system.
is a Peano system.
The following theorem expresses the structural similarity between this Peano system and the 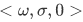 .
.
Theorem 4H Let  be a Peano system. Then
be a Peano system. Then 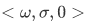 is isomorphic to
is isomorphic to 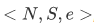 , i.e., there is a function h mapping
, i.e., there is a function h mapping 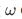 one-to-one onto N in a way that preserves the successor operation.
one-to-one onto N in a way that preserves the successor operation.
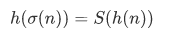
and the zero element
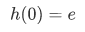
Remark: The equation 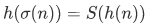 together with
together with 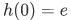 implies that
implies that 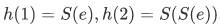 . This can be shown as follows,
. This can be shown as follows,
Theorems 4D and 4H relate the constructive approach to the natural numbers and the axiomatic approach. Theorem 4D shows that Peano's postulates are true of the number system we have constructed. And theorem 4H shows that the number system we have constructed is, "to within isomorphism," the only system satisfying Peano's postulates.
Disclaimer: this is a summary of section 4.3 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...


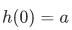
Nice post ! You got 19.45% upvote from @flymehigh. Earn free sbd/steem daily by delegating(renting) your SP. We share high return, click here to delegate your sp to flymehigh if you don't know, how to earn passive income by delegating your SP click here for more info Join our discord You can promote your posts. Thanks.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@tipu profit 1000 sp delegated
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yesterday 1000.0 STEEM POWER delegated or invested gave payout of:
0.014 SBD + 0.46 STEEM (0.15 USD), APR: 18.39% .
Delegation link: steemconnect 1000.0 SP delegation to @tipu.
Please note that your profit can be slightly different (depending on the payout time).Check out https://www.steemprofit.info to compare @tipU with other services.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@tipu profit 1500 sp delegated
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yesterday 1500.0 STEEM POWER delegated or invested gave payout of:
0.021 SBD + 0.69 STEEM (0.22 USD), APR: 18.39% .
Delegation link: steemconnect 1500.0 SP delegation to @tipu.
Please note that your profit can be slightly different (depending on the payout time).Check out https://www.steemprofit.info to compare @tipU with other services.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit