Elements of Set Theory: Relations
First let's consider some examples.
The ordering relation < on the set 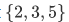 is one example. We say that < relates each number to each of the larger numbers. We can visualize this relation by drawing some arrows to each relation.
is one example. We say that < relates each number to each of the larger numbers. We can visualize this relation by drawing some arrows to each relation.
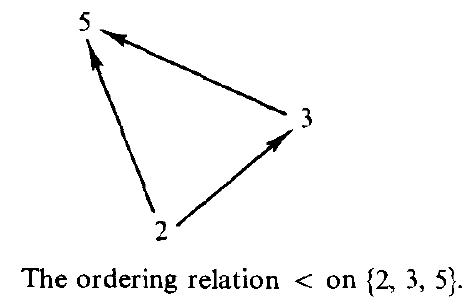
Thus we can say, that
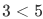 , relating 3 to 5. For this case, we have an arrow from 3 to 5.
, relating 3 to 5. For this case, we have an arrow from 3 to 5.
What set adequately encodes this ordering relation?
Using the arrows as guide, we take the ordered pairs 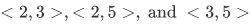 . The set of these pairs
. The set of these pairs
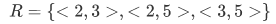
completely captures the information. R is the ordering relation on 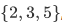 , consists of the pairs tying each number to the larger numbers; a relation is this collection of "ties".
, consists of the pairs tying each number to the larger numbers; a relation is this collection of "ties".
A close the heart kind of example might be the relation of marriage. This relation is the aggregate total of individual ties between each married person and his or her spouse. Or to state it more mathematical, the relation is,
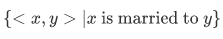
From here I want you to see that a relation will be a set of ordered pairs. And there are no other conditions, as long as we have an ordered pair it is some relations, even if peculiar one.
Definition A relation is a set of ordered pairs.
Sometimes we write relation R as follows: 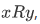 instead of
instead of  .
.
Consider the ordering relation < on the set 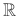 of real numbers,
of real numbers,
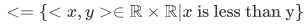
For this case, we would prefer to use the notation 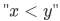 than
than 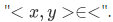 .
.
Some relations are more interesting than others, in the coming future posts we are going to look at functions, equivalence relations, and ordering relations. At this point, we make some general definitions.
Definition We define the domain 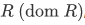 , the range of
, the range of 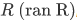 , and the field of
, and the field of 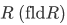 by
by
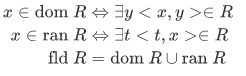
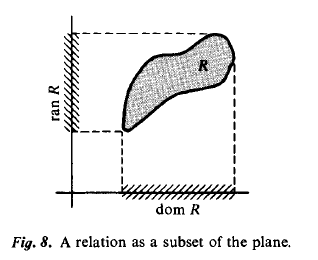
One good illustration of the definition above is the set
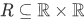 . Then R is a subset of the coordinate plane. The projection of R onto the horizontal axis is dom R, and the projection onto the vertical axis is ran R.
. Then R is a subset of the coordinate plane. The projection of R onto the horizontal axis is dom R, and the projection onto the vertical axis is ran R.
Disclaimer: this is a summary of section 3.2 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora
Thank you for reading ...


You got a 3.52% upvote from @minnowvotes courtesy of @sinbad989!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You got a 22.99% upvote from @moneymatchgaming courtesy of @sinbad989! Please consider upvoting this post to help support the MMG Competitive Gaming Community.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit