Welcome to our lessons on proportions Part 2 is our second lesson on proportion to kinda goes hand in hand with a lesson that we had the other day which is proportions part 1
The first question or type question that we're gonna look at is when you have a proportion are to equivalent fractions and you need to solve for that variable we need to find out what and is to do that we use something called cross multiplication in other words we're going to multiply 10 times and across their and 20 times 5 across their
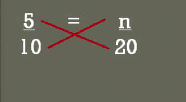
And you see it makes across and that's probably the reason why they call it cross multiplication 20 times 5 is 100 10 times n is 10n
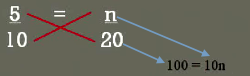
And it will divide each side by 10 that will help us to isolate are variable by itself on the right hand side the equal sign and we now know 10 is equal to n so such thing as that 10 over 20 is the same 5 over 10 so that are our proportion we solve for the variable that was there

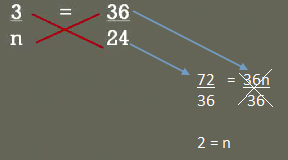
The next one shows a little bit more practice in this one I register the variable to the bottom, but it's going to be the same type of question we're going to use again cross multiplication well, we multiply n times 36 and 24 times 3, 24 times 3 is 72 and 36 times n is 36n to stall for the variable and will divide both sides the equation by 36, we will cancel the 36n over 36 And 72 divided by 36 is 2 so 3 over 2 is equal to 36 over 24 those are equivalent fractions equivalent ratios or in other words the proportional to each other their Proportions.
Ok, now some practical questions using proportions look at help us to to give a practical application if you have 50 gum balls and cost you $12.50 how much Would it cost to buy 7 gum balls? I've been set up my fraction first 50 over 12.50 I put the number gumballs on top and the cost on the bottom
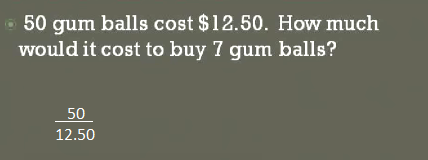
So the nest fraction and I'm doing, I am going to set up the same way that number of gumball on top and the cost on the bottom we don't know the cost some going to simply put in the variable C that's what we're looking for
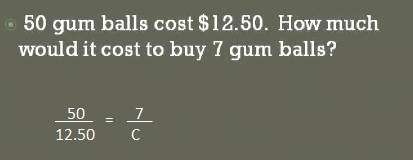
Now this looks familiar this is a proportion that we can solve just like we did last one using cross multiplication
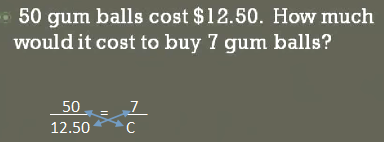
So start out by multiplying C times 50 it gives me 50c and then I'm going to
Multiply 12.50 Times 7 that gives me 87.50 dollars

Now to isolate the variable of C by itself, I have to divide both sides by 50.
50c over 50 cancel each other out and end up with C be equal to one dollar 1.75. 7 gum balls cost $1.75

The key to success in proportion is making sure that your fractions are the same if you have miles Over hour you have miles over hour ok

A distance and a time like the one here we have a distance and a distance and a time and a time it that does not work you have to have the same measurement in both

You have to have miles and miles hour and Hour if you're going to do kilometers and minute You do do kilometers and minute so that the fractions are the same that's the key to success in proportions
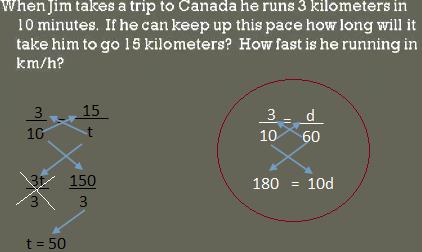
I'm gonna show you an example that right Here of kilometers and minute When Jim takes a trip to Canada he runs 3 kilometers in 10 minutes if he here in America, he'd be running miles per hour something miles per minute I don't know, but he goes to canada and he runs 3 kilometers in 10 minutes that is my fraction so I have kilometers on top Minutes at the bottom ok

If he can keep up this pace how long will it take him to go 15 kilometers, so 15 kilometers and T the amount of time we don't know the time that's the proportion that we have set Up

So that we can use our cross Multiplication

Where we say 3 times 3 is 3t, And 10 times 15 will give us 150 isolated 3t over 3 going to divide both sides by three we end up with a final answer that T is equal to 50

What that means in words is Jim runs, 15 kilometers in 50 minutes 50 kilometers per 15 minutes
That's not usually the way we talk so I actually added on a question here how fast is he running in kilometers per hour, so now we're gonna have to do a second proportion actually find out how many kilometers is it per Hour I gonna do the same thing I did before here where I start with 3 over 10 he's running three kilometers in 10 minutes

What I'm searching for is how many so like distance i call it D how many kilometers will he run In 60 minutes

That's the trick with this one we have Kilometers and minutes we need to have kilometers And minutes we know that 60 minutes is equal to 1 hour so how fast he is running in one Hour. D over 60 is the distance that he will run into 60 minutes, that's the key right there and you'll see a lot of questions like that works converting from minutes to hours or hours to minutes and the key is that you use the same measurement so in this case I have it all in minutes I'm gonna say 60 minutes when I talking about an hour as do the same thing.
Cross multiplying 60 times 3 is 180, 10 times D is 10d
Divide both sides by 10 to find the distance. 18 kilometers equal to D
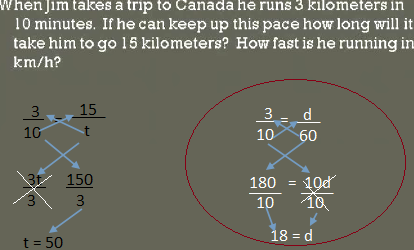
The Jim is running 18 kilometers per hour.
So we actually done 2 proportions here, but in both cases we make sure that we Have kilometers on the top minutes on the bottom and you'll know the key to being successful is setting up your proportions the same on the top as on the bottom in both fractions alright
It is the end of today's lesson I hope that it's been helpful for you