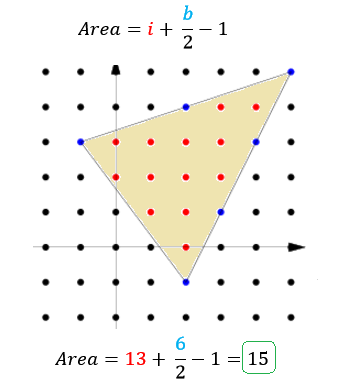
Need to find the area of a simple polygon? Have a lattice board? I have a formula for you!
Pick's formula, that is. This universal area formula for lattice polygons is as equally accurate as it is jaw dropping in its simplicity. Take a geoboard, or coordinate plane with equally spaced grid points, draw a polygon of arbitrary size on that board, and count the points on the boundary and interior of the shape. The area of said shape?
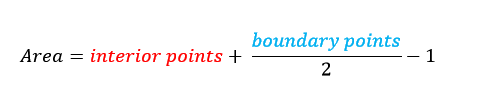
It's hard to believe, but this formula seriously works no matter the case:
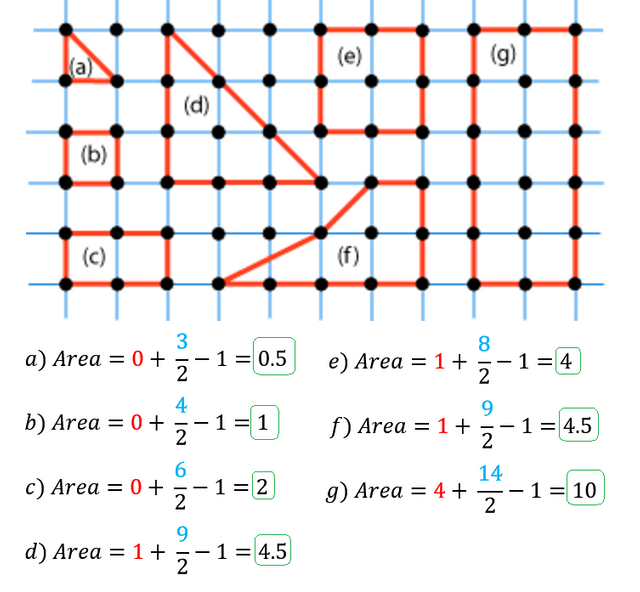
And, a few of you out there are probably thinking "eh, he just set those up to be 'conveniently' on the coordinate grid." And, in a way, yes you are correct. The stipulations behind this formula include:
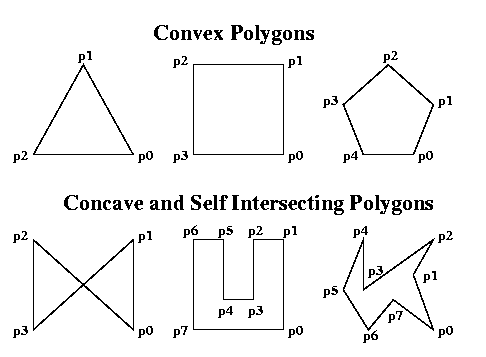
- The shape must be a polygon. It can be concave or convex, but not self-intersecting. No circles apply here, sorry!
- Each vertex of the polygon must fall on the board.
- The polygon must be complete. No holes. Although, if it does have a hole, we can still compute area by subtracting the smaller area from the larger area IF the interior hole is also a lattice polygon.
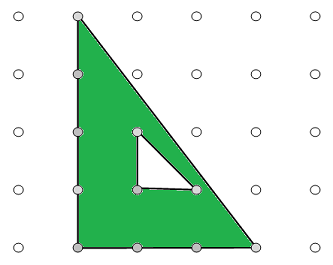
- Pick's formula assumes unit measures and unit squares for area. You can make your unit whatever you desire though if sides of your shape aren't whole numbers. However, you must adjust the value of your unit squares accordingly. So, if you made your lattice units 0.5, your interior squares would each be
0.5*0.5=0.25square units each.
So, it does have some prerequisites. However, the fact this holds is a minor miracle, and even has applications well beyond area. It's founder?
Georg A. Pick

Pick was described as "...a bachelor ... uncommonly correct in clothes and attitude (source)."
He entered the University of Vienna in 1875, and was quite skilled in both math and physics, later being certified to teach in both areas. Pick studied or worked with many a notable mathematician of his day, but his claim to fame was being the driving force behind the committee decision to appoint Albert Einstein to the University of Prague.
Pick and Einstein were colleagues, friends, and even passionate musicians.
Not only did they share scientific interests, but they also shared a passionate interest in music. Pick, who played in a quartet, introduced Einstein into the scientific and musical societies of Prague. In fact Pick's quartet consisted of four professors from the university including Camillo Körner, the professor of mechanical engineering. (source)
Like many an artist, Pick never got to live to see his formula achieve the status it has today. It was not really received with much attention at the time, and sadly Pick died an early death in a concentration camp during World War II.
As for what made it popular?
The result did not receive much attention after Pick published it, but in 1969 [Hugo] Steinhaus included it in his famous book Mathematical Snapshots. From that time on Pick's theorem has attracted much attention and admiration for its simplicity and elegance. (source)
Seriously though, how does this thing work?
To prove Pick's Theorem, we need to make a case for "easy" shapes first. Shapes like rectangles and triangles. Then, we will expand our focus outward to any polygon.
Generally speaking, we will show that when Pick's Theorem is applied to a shape, it will yield the same formula we are used to for that shape.
Case 1: The Rectangle
Ahh, the nice, friendly rectangle. This is the easiest case to understand because of the way we can nicely count boundary and interior points.
Boundary points are given to us by finding the perimeter of the shape. Interior points are determined by multiplying one less than the dimension of the base and height by one other. If we take the general expressions for each of these for a j x k rectangle and substitute into Pick's Formula, we would expect to get the area formula for a rectangle, Area = j * k.
Spolier alert: We do.

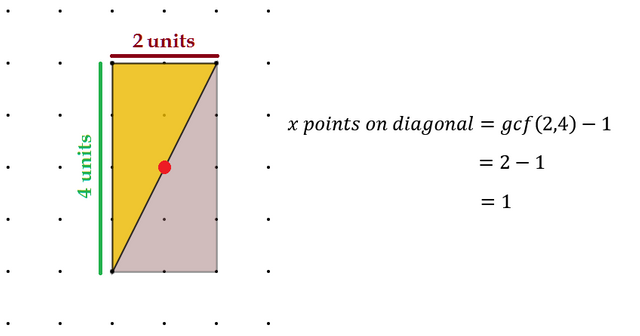
Case 2: The Right Triangle
The right triangle can be thought of as a general case of a rectangle, just cut in half down a diagonal. Again, we desire a relationship between interior and boundary points that would show a generalized area formula for a triangle, A=(1/2)bh.
It gets tougher to count boundary points this time because of the diagonal. It does take a little mathematical poking and prodding to reveal the points on the hypotenuse, those that are not the endpoints anyways. We have to determine this by finding the greatest common factor of the dimensions of base and height and subtracting 1.
For a j x k rectangle in general, this will make our formula for boundary points:
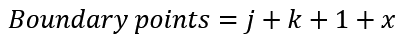
Remembering that a right triangle is half of a rectangle will assist us greatly in finding interior points. We take our previous formula for a rectangle, (j-1)(k-1), subtracting x points on the diagonal that weren't part of the rectangle formula, and divide by 2.
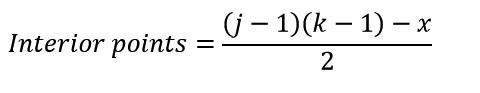
Great! Now let's piece these two formulas together and see if we get the area formula for a triangle, (1/2)*base*height
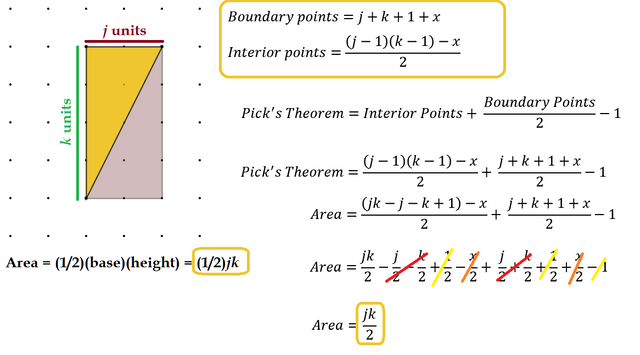
SWEET!
Case 3: The General Triangle
We are starting to loosen the reigns a little bit here! If it wasn't already with our last example of the right triangle, it is going to become painfully obvious that if we are going to solve a complicated problem, we have to start solving a series of easier problems first. Namely, compare every possible triangle back to the easiest shape of a rectangle.
If we do this, we start to reveal really cool patterns like the one below. We take our desired yellow triangle T and make a rectangle out of it by surrounding it with two others that would all sum together to a rectangle.
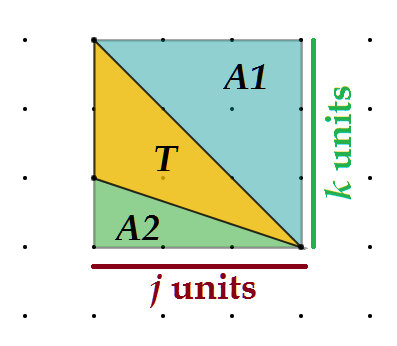
Note here, we will define A1 and A2 as the areas of the two right triangles that surround our general triangle. Here, we would love to show:
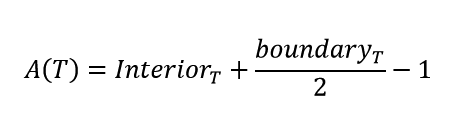
And, we already know that for A1 and A2 Pick's formula holds, as they are right triangles and we have already shown that result. We also know for the overall rectangle Pick's will hold as we have shown that as well. Therefore, we can utilize Pick's formula for each of the shapes in our diagram as follows:
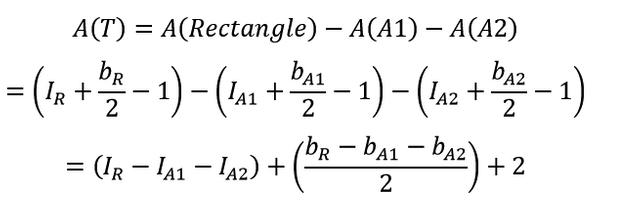
Remember that for the jxk rectangle, the area will be jk, the boundary points will be 2j+2k, and interior points will be given by (j-1)(k-1). Putting this all together carefully with our prior definition of boundary points for the longest side of right triangles yields:
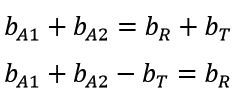
Counting interior points carefully of the rectangle, and subtracting 3 because the corners of the triangles are double-counted, will yield:
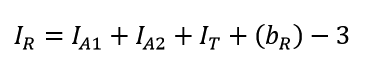
Now, we substitute equations and solve! Our mystery triangle? Turns out Pick's Formula applies for it as well.


Other Shapes?
It turns out that since every two dimensional polygon can be partitioned into triangles, Pick's formula holds for them as well.
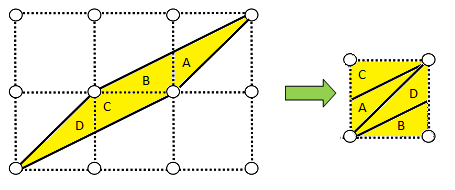
The proof of that? Well, it involves mathematical induction, and something well out of the scope of this post. But, you can think it kind of like climbing a ladder.
If you can get on the first step and can show you can get to the next, induction would suppose you could get to every step on the ladder. Our "easy" cases from earlier were the base case steps that enabled us to show Pick's Formula held. To show others, you just need to handle how any shape in general could be split into the basic shapes from the base case. I submit this excellent paper as proof, if you so desire to see.
__
So, next time you see an unfamiliar shape, put it on a lattice.
Impress your friends and family with your new found knowledge. Because when they are scrambling with rote memorization of area formulas from the ghosts of Geometry classes past, you will be the Usain Bolt of the formula world.

Want to play around more with Geoboards and lattice polygons? Try this tool here! It is also how I generated many of the polygons you see in this post.
Image Sources
- Georg A. Pick
- Pick's Examples
- Concave/Convex Polygons
- Thumbs Up GIF
- Partitioned Triangles
- Usain Bolt By Erik van Leeuwen, attribution: Erik van Leeuwen (bron: Wikipedia). - erki.nl, GFDL

Dude, you're going on my auto-upvote list. When I roll out my upvote bot in a couple weeks. This stuff is awesome. You teach, right? What level? I've been fantasizing for a couple years about creating a course called something like Weird Math for Non-Majors. We'd basically just talk about stuff like this, and infinite cardinals, and high dimensional geometry paradoxes, and generalized inverted pendulums. It would be an exercise for me in explaining bizarre unintuitive theoretical concepts to people in intuitive ways.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
First, thanks for the kind words! I always aim to explain the crazy scary concepts in math in intuitive ways, so your compliments come as high praise! I am indeed a teacher, high school and adjunct college.
The kind of course you are describing sounds amazing! The closest thing I have seen in my location is just a generic math topics course, with clubs like math circles taking up many of the interesting topics not covered in standard classes. Which, truly is a shame because so much of this kind of math is very beautiful but very intimidating. The on ramp to this kind of stuff needs to be much more approachable for someone just looking to study as an elective and seem as sexy as studying a science. Anything that gets students there I would sincerely applaud.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Have an upvote. lol.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I vaguely remember pick's theorem but this post taught me more about it than I had learned in school. I love your writing style. Technical but straight-forward,. A++
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks! It taught me more than I learned in school too ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I never actually learned about it in school, even though I was in a math specialization. I wonder how many such math wonders are hidden from the public eye. you did an amazing job with this post @team-leibniz. kudos for the illustrations as they add a great layer of understanding for your explanations.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks! I look forward to writing about more!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Really great post, I actually never knew about doing all of this with lattices, and it does make certain problems seemingly much much simpler to tackle. I will likely have to re-read this again to better absorb the information. Math is not as easily internalized for me as other disciplines.
Fantastic job with the presentation as well. Loving the illustrator diagrams. :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks! Many were made with the geoboard applets that exist out there on the internet like the one here.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Oh very cool! Didn't know these existed either. Might come in handy for me as I progress through my own series if I need correctly sized polygons! Thanks!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Fantastic! A concrete method to show my students. Thanks!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I like this a lot. First time I've heard of it. Thanks!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been linked to from another place on Steem.
Learn more about linkback bot v0.3
Upvote if you want the bot to continue posting linkbacks for your posts. Flag if otherwise. Built by @ontofractal
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit