The Pythagorean Theorem - A Collection of History, Proofs, Demonstrations, and Oxen Sacrifices

You all know it, you love it, you couldn't do without it. Quite possibly the most famous theorem of all time. The Pythagorean Theorem:

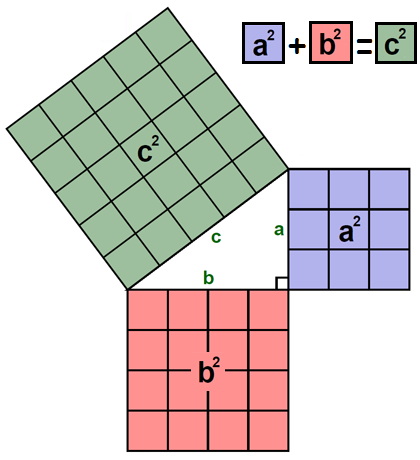
The fact that a² + b² = c² has probably been tattooed in your heads since you sat through your first early education math course. So much so, it's almost a meme at this point. Oh yeah, it actually is:

A little Pythagorean history

Pythagoras (569-500 B.C.E.) was born on the island of Samos in Greece. Little is known really of his early years, but he gained his status at the time for founding a group, nay brotherhood, of like minded individuals to engage in mathematical pursuits. Their creative name?

The Brotherhood of Pythagoreans

This group was more cult than clique. They had their own symbols, rituals, prayers, and routines. If Stanley Kubrick were alive, there is no doubt he would be writing a script about them right now.

Because of the mystery surrounding this group, the discovery of one of the most famous theorems of all time is also shrouded in mystery. Most history surrounding this is equal parts guess work and tall tales.

For one, Pythagoras was credited with the discovery of this theorem, even though it is not possible to tell if he or one of his "Pythagoreans" penned it. This group also really believed in the magic of numbers and shared a vow of secrecy regarding discoveries about said magic. So, the discovery of anything truly historical would have most likely been kept within the fold.

I mean, we are talking about a group of people that put to death a member who dared to out the "discovery" of irrational numbers through manipulation of triangles! It is also the same group that allegedly watched its leader sacrifice over 100 oxen after the discovery of the theorem. So, to say these people were creepers is a colossal understatement.

Ignoring the creepiness of the Pythagoreans, let's focus on the beauty of the theorem and the inspiration it has provided for generations.

Want to make sure you have a right angle? Then measure 3-4-5. Want to find the coordinates of any point on a circle? A sphere? Find the shortest distance between two points? The applications are limitless.

The proofs? Even better.

There are literally hundreds of them out there. Below are a collection of just some of my favorites.

An intuitive approach, with four right triangles.

Take four carbon copy right triangles and arrange them all to form a large square. Note, we can guarantee this will be a square because every side will have length c and the sum of the other two non right angles must be 90°.

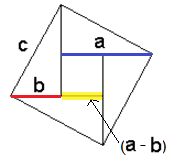
Now time to put it all together:

• Every triangle on the outside has has area ab/2. There are four of these, so all four have area together of 4 * ab/2 = 2ab
• The inner square hole with side length (a - b) has area (a - b)² = a² - 2ab + b²
• We can think of the big square, consisting of four triangles and one "tiny" square, as having combined area of: 2ab + a² - 2ab + b² = a² + b²
• But, the outermost square with side length c must also have area c². And it "contains" all of our five tinier shapes.
• Since these two must geometrically equate, a² + b² = c²

---

This next one was discovered by...President Garfield?!?!

Yep. Former U.S President James A. Garfield was at one point in his life an aspiring mathematician. He studied math even after he decided to run for Congress and would even discuss it on the floor with other U.S representatives.

If it was anything like my discussions with colleagues about math, it probably was a one way endeavor. Let's face it, math isn't the sexiest thing to talk about.

But, during one such conversation, legend has it inspiration struck and he came up with the following brilliant proof of the Pythagorean Theorem. So brilliant, in fact, that it went on to be featured in the New England Journal of Education in 1876.

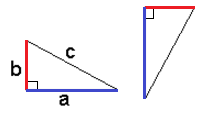
This time, take two carbon copy right triangles and arrange them as 90° of each other. Connect as follows:

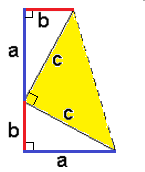
Note that if you connect two of the vertices (I did so with a dashed line above), it creates a third right triangle with each leg of length c.

However, if you step back and consider the entire shape as a whole, it is a trapezoid!

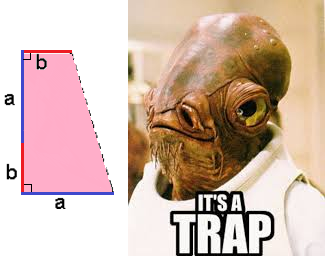
Now time to put it all together:

• The area of a trapezoid is (1/2)*height*(base1+base2). For our trapezoid, that makes (1/2)*(a + b)*(a + b)= (a² + 2ab + b²)/2
• But, the trapezoid area must be equal to the area of the sum of its parts, the three right triangles!
• The two original right triangles each have area ab/2. The "phantom" right triangle has area of c². Together? 2(ab/2)+c² = ab+c².
• Now, let's equate and solve!

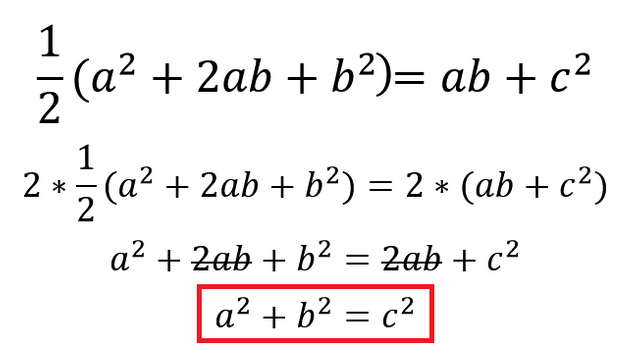
EDIT 1: @neoxian gets the gold star for reminding me I originally omitted a parentheses above. Now fixed.

---

As you can see, the Pythagoreans were a clever bunch of creepy oxen sacrificing mathematicians.

And, I wouldn't have it any other way. Makes teaching this thing every year so much more entertaining.

In closing, a little video demonstration for good measure:

---

EDIT 2: I need to provide a PROPER image credit and shoutout for the lead image to J.A. Knapp, the illustrator of the cover photo from Manly Palmer Hall's The Secret Teachings of All Ages. It turns out, our very own @reneenouveau, aka @illuminaughti on steemit.chat, is related to the original artist of this 1927 illustration (Great Great Great Grandfather)!

---