Thanks to a video I saw on Youtube, I know now a way to prove both the relations I used in this post.
First a few notations: Given a closed simply connected (without holes) domain on the plane, let B > 2 be the number of edges and of vertices of its boundary:
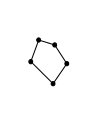
Here, B = 5.
I first quickly prove that it is always possible to triangulate this domain by adding B - 3 internal edges to get B - 2 triangles:
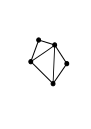
Here I added B - 3 = 2 internal edges to get B - 2 = 3 triangles.
It is obviously true in my example and even more simply in a triangular domain where not adding any edge gives one triangle already.
Then, by induction, suppose that I have a total triangulation with B vertices, 2B - 3 edges (B on the boundary and B - 3 inside) and B - 2 triangles. I need to prove that I can construct a triangulation with B + 1 vertices, 2B - 1 edges (B + 1 on the boundary and B + 1 - 3 inside) and B - 1 triangles (B + 1 - 2). And indeed, I choose any edge on the boundary, let T be the triangle including that edge. I add a vertex on it (so B + 1 vertices and 2B - 2 edges for now). Then I link this new vertex with the third top of T, the one that is not on the chosen edge. So I have a new edge (that's 2B - 1 of them now) and T has been split in two so that's one more triangle, which makes B - 1 as expected:
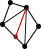
Now the fun part ! (no proof though)
Suppose, as before, we have a closed simply connected domain on the plane. Let B > 2 be the number of edges and of vertices of its boundary but suppose now on the contrary that it is totally triangulated with V vertices (B around, V - B inside), E edges (B around, E - B inside) and T triangles.
Then the two relations (amazingly generalized in any dimension, nothing less) given in this post are given by the
Dehn–Sommerville theorem (1927):
The h vector is symmetric
Simple isn't it? But, what is the h vector?
It is really really cool :-)
First, we need to create a triangulation of the sphere. Don't panic. Since we're dealing with a topological sphere, our simply connected domain is already a triangulation of half a sphere! But remember, we can easily create a triangulation of the other half. Just take the same boundary with B vertices and B edges, add B - 3 internal edges and enjoy the B - 2 triangles.
Then we join the two halves along the common boundary, et voilà, a triangulation of the sphere with f0 = V vertices, f1 =E + B - 3 edges, f2 =T + B - 2 triangles.

And now, built this triangle:
1 1 f0 1 f0-1 f1 1 f0-2 f1-(f0-1) f2 1 f0-3 f1-(f0-1)-(f0-2) f2-(f1-(f0-1))
That is like a Pascal's triangle except the right diagonal is the fis in order and the rule is subtract left from right instead of adding them.
The last line is the h vector!
So, according to Dehn–Sommerville theorem, f2 - (f1 - (f0 - 1)) = 1
That is T + B - 2 - (E + B - 3 - (V - 1)) = 1. Hence
T - E + V = 1
But, thanks to this theorem, we have also f1 - (f0 - 1) - (f0 - 2) = f0 - 3
That is E + B - 3 - (V - 1) - (V - 2) = V - 3 and, as V = E - T + 1,
B = 2E - 3T.
How deep is that?