Mathématiques : algèbre linéaire 1 - Qu'est-ce qu'une famille libre ou liée ?

Aujourd'hui je vous propose un post un peu plus difficile, à savoir une petite introduction à l'algèbre linéaire de manière concrète et plus particulièrement : qu'est-ce qu'une famille libre et une famille liée ?  

L'idée est d'essayer de vulgariser la chose donc je vais volontairement ne pas être super rigoureux histoire d'être un minimum accessible. On se passera du même coup des notations vectorielles ainsi que des définitions abstraites. Le but est de pouvoir approcher cette discipline de manière intuitive.  

Pour rappel, l'algèbre linéaire est une section des mathématiques qui a pour vocation l'étude des espaces vectoriels et toutes les transformations dites linéaires. Il s'agit d'une discipline fondamentale dans le monde moderne qui nous entoure.  

Prenons un exemple trivial et considérons les deux vecteurs, dans R2, de la base canonique (1;0) et (0;1). Ils sont précisément une famille libre et nous allons essayer de comprendre pourquoi. 

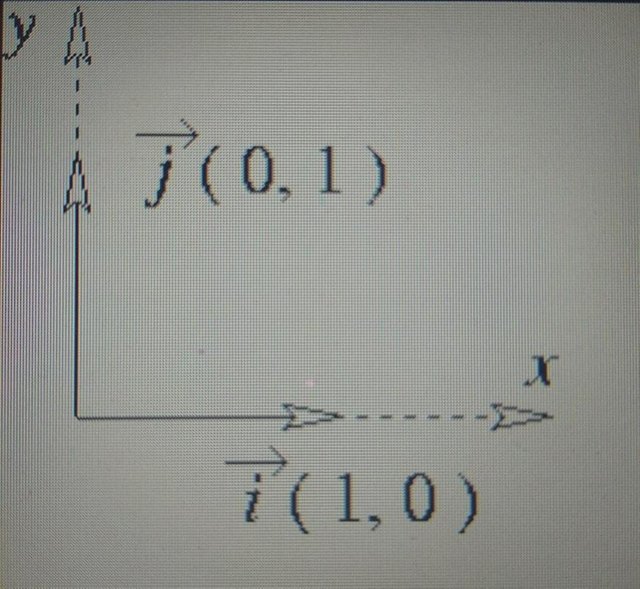
Vecteurs de la base canonique dans R2

Les vecteurs d'une famille libre sont, par définition, linéairement indépendants. Cela signifie, pour faire simple, qu'on ne peut pas exprimer un vecteur en fonction des autres.  

Un contre-exemple : prenons le vecteur u = (1;1;2) et le vecteur v = (4;4;8) dans R3.  Nous avons v = 4u (la notation ici est abusive, comme dit en préambule) Nous avons pu exprimer v en fonction de u , par conséquent la famille n'est pas libre. On dit dans ce cas qu'elle est liée.  

Qu'en est-il de nos 2 vecteurs de la base canonique i = (1;0) et j = (0;1) ?  

Intuitivement, nous voyons bien qu'il va être difficile de réussir à exprimer l'un en fonction de l'autre. Comment en être sûr ?  Essayons de trouver un x et y dans R tel que : 

x(1;0) + y(0;1) = 0  

Pourquoi ? Si nous parvenons à trouver un x et un y différent de 0 nous aurons :  

x(1;0) + y(0;1) = 0  

x(1;0) = - y(0;1)   

(1;0) = -y/x (0;1)  

i = -y/x (j) et nous avons réussi à exprimer i en fonction de j, ce qui donnerait une famille liée (avec x et y dans R*)  

Allez c'est parti, examinons la chose :  
  

x(1;0) + y(0;1) = 0 revient à résoudre le système :  

x + 0(y) = 0 et 0(x) + y = 0  

Nous avons donc x = y = 0 , la combinaison triviale.    

Ceci veut exactement dire que la famille est libre et que les deux vecteurs sont linéairement indépendants, ne pouvant pas être exprimé l'un en fonction de l'autre.  

Lorsqu'il n'existe pas d'autres solutions que la combinaison dite triviale, la famille de vecteurs est libre. En plus rigoureux, si les coefficients, de la combinaison linéaire des vecteurs égals au vecteur nul, sont nuls, alors la famille est libre.  

Et voilà c'est pas plus compliqué. Bien évidemment, il s'agit d'un exemple basique, on peut ensuite faire pareil dans R3 avec des vecteurs qui ne sont pas forcément ceux de la base canonique, travailler dans R[x] qui est l'espace des polynômes, s'amuser avec des matrices ou des suites numériques, bref tout est possible.  

Si vous vous demandez à quoi sert une famille libre, j'y répondrai dans un prochain post !