Hello, this is @doctorbme. Today’s topic is a little less complex.
When dealing with machine learning, we come across 'bias-variance trade off' at least once. When training an algorithm, the bias that reflects how far the prediction of the trained algorithm is from the answer and the variance that reflects how big the range of fluctuation is for the prediction are in a trade off relationship. Because the sum of these two values ultimately determine the error of the algorithm that we predict, it is important to appropriately balance these two values.
Let’s take a look at the figure below for a better understanding.
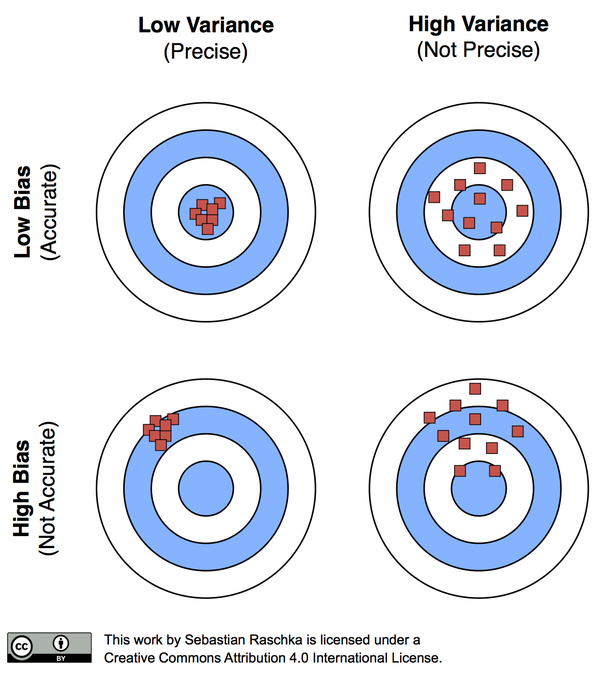
Figure 1. Concept of bias and variance (concept of accuracy and precision)
As shown in the top left figure, it is most ideal when the points are tightly packed together and accurately fall in the target. But, as shown in the bottom right figure, the algorithm can be considered to have failed when the points are off the target and spread apart as well. Usually, results group together well but miss the target (large bias: bottom left figure) or the results are near the target on average but the predictions are dispersed (large variance: top right figure).
Because bias and variance are in a trade off relationship, the most important thing is creating a good balance between them as variance can increase when attempting to decrease bias and vice versa during the process of training an algorithm.
For example, when we think about a problem of classifying two classes on a 2-dimensional plane, we can observe that the performance changes depending on what boundary we set to classify the classes.
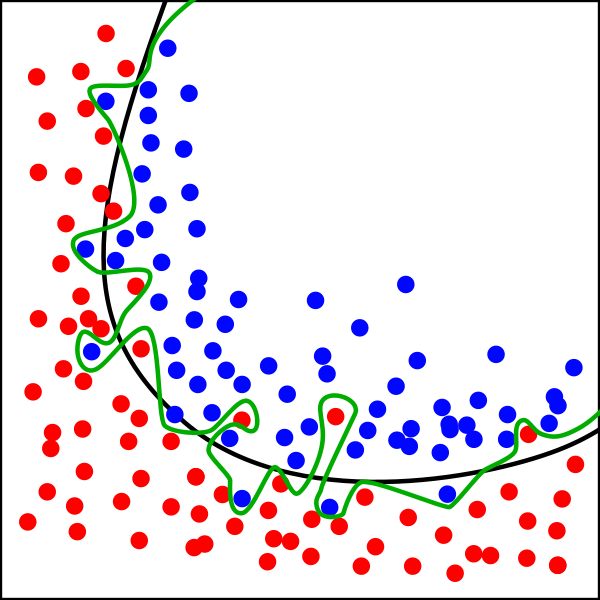
Figure 2. Setting two types of boundaries to classify two classes
In the above figure, most will think about making the training data as red and blue dots and a black line for classifying the domains. It is natural to imagine that a certain smooth boundary exists. It is ok to set the green line as the boundary, but even if the error turns out to be almost 0 in terms of the given training data, the existence of another training set will create a deviation between the trained models. In other words, the shape of the boundary will be very crooked every time the training data set changes, which means the dynamic range of the boundary’s shape can expect to be very diverse. In other words, the model’s variance will be increased.
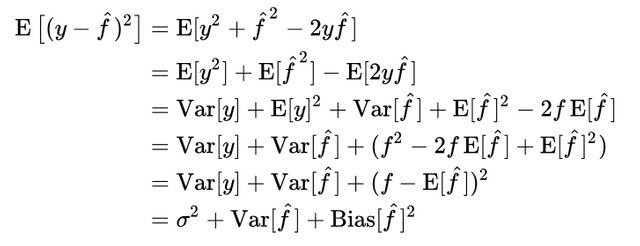
Ultimately, the global error appears as shown above. The first section is the error which we cannot reduce. Second is the distribution of prediction models themselves. Third reflects the bias, which is the difference between the correct (true) model and the expected value of the prediction model we are seeking. The reason why we implement model learning is because we are ultimately oriented toward minimizing the global error, and when the global error is given, a bias-variance trade-off occurs in between. (One thing to note here is that the training data itself may not be just one meaning many training data sets may exist, and models on such data sets may have their own expected models.)
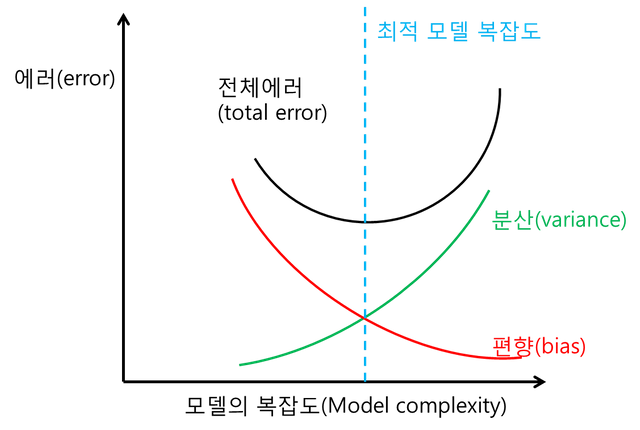
Figure 3. Relationship between total error, variance, and bias
Now, we realize that an appropriate model ultimately means finding the optimum complexity that does not lean to one side through consideration of the balance between variance and bias. Contrastingly, however, we can also realize that having a very small bias or very small variance is also not the optimum situation.
No matter what the issue is, I believe we need to consider such relationship between bias and variance. When we view an issue too simply, it is convenient to unify the opinions but we might end up getting answers that are somewhat off the actual truth that we were looking for. On the other hand, when we view an issue too complexly, it is convenient to reflect the diversity of opinions and find the center but it might be difficult to unify the opinions. (Or extremely high cost might be required to gather the opinions.) Therefore, going after unconditional unification of opinions or very high diversity of opinions may ultimately break the balance.
Such issues can apply to each person gathering opinions on a certain issue or in terms of making decisions toward a direction and experiences in our lives. If we continuously make biased decisions in our lives, it may be difficult to realize the diversity and variety that our lives offer. And if we continuously focus only on diverse experiences, it may be difficult to maintain the center of our lives for taking each step forward toward a certain path. (Or we may have to experience many trials and errors.)
In the end, we have to think about the following perspectives concerning the above facts.
- Whether it is about training, issue, or life, a unique error that inevitably occurs will exist. It is necessary to accept that a certain amount such errors exist.
- It is impossible to perfectly remove bias or variance. Such direction may rather put us at risk. We must always find a balance between bias and variance.
This seems to be the message of bias–variance trade off.
Figure reference
Figure 1, https://sebastianraschka.com/blog/2016/model-evaluation-selection-part2.html, Creative Commons 4.0 - BY
Figure 2, https://en.wikipedia.org/wiki/Overfitting , Creative Commons 4.0 - BY SA
Figure 3. Self-made

Congratulations @mediteam! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - The results, the winners and the prizes
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit