Bài viết ngắn này nhằm phân tích Bitcoin dựa trên quy luật cung và cầu, có khá nhiều phát hiện thú vị khi áp dụng định luật Metcalfe.
- Trước tiên tôi đã tiến hành phân tích thống kê sơ bộ và đưa ra lý do về việc lựa chọn mô hình, sau đó tôi thảo luận tại sao ứng dụng hoặc mô hình trực tiếp dựa trên định luật Metcalfe có thể không chính xác, và tại sao nếu bạn thiết lập mức rủi độ rủi ro và sử dụng mô hình giá mà không quan tâm đến quy luật này sẽ khiến bạn thất bại. Tiếp theo tôi cũng sẽ đưa ra một số ví dụ về mô hình mô phỏng trong bài viết này.
- Tiếp đó sẽ là việc giải thích về mối tương quan nội tại giữa tài sản crypto với biến động của mạng lưới.
- Cuối cùng, tôi kết hợp mô hình giá nhằm ước tính số lượng tất cả các địa chỉ để mô phỏng các đường giá có thể diễn ra trong 03 năm tới.
Mô hình Lựa chọn và phân tích dữ liệu sơ bộ:
Trước hết, mô hình cung và cầu của bitcoin có rất nhiều dạng khác nhau. Tôi đã dành nhiều nỗ lực để chọn một dạng mô hình mà tôi có thể xử lý. Và tôi thu hẹp phạm vi viên nghiên cứu của mình xuống với 02 yếu tố.
Số lượng địa chỉ Bitcoin hoạt động và tổng số địa chỉ Bitcoin.
Dữ liệu tôi đã sử dụng là giá bitcoin và số lượng địa chỉ Bitcoin từ ngày 29.11.2011 đến ngày 22.05.2018, được tải xuống từ blockchain.info. Khoảng thời gian giữa các điểm dữ liệu là 02 ngày. Địa chỉ hoạt động được định nghĩa là địa chỉ đã thực hiện giao dịch trực tuyến trong vòng 24 giờ qua. Tôi đã chọn số lượng tổng số địa chỉ Bitcoin vì lý do sau.
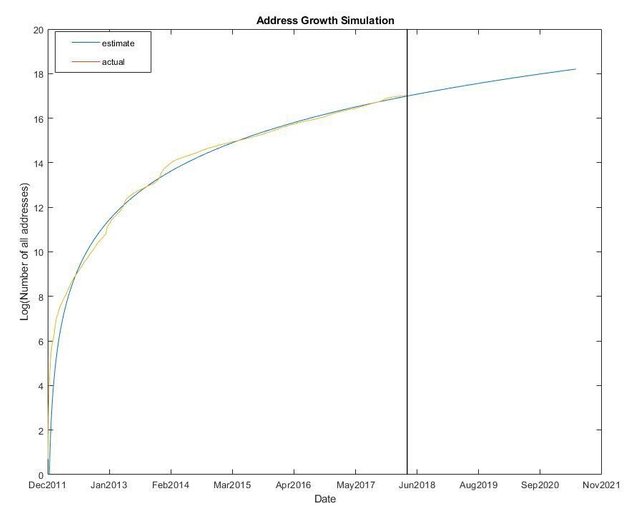
Thứ nhất, số lượng các địa chỉ đang hoạt động khó dự đoán hơn, trong khi tổng số ví là một đường cong tăng lên, xem hình bên dưới.
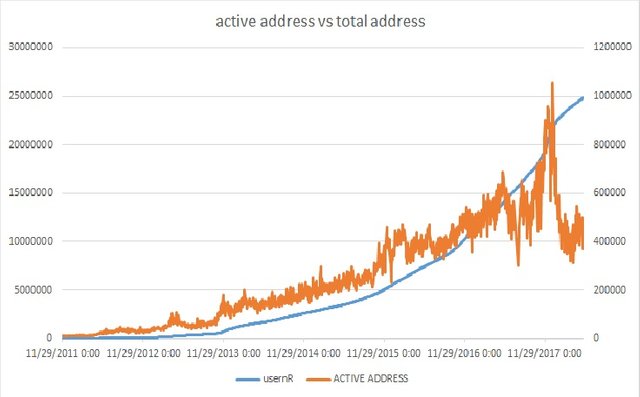
Số lượng tất cả địa chỉ tăng đều đặn hơn số lượng địa chỉ đang hoạt động. Trong đó số lượng tổng địa chỉ trên trục Y bên trái và Số địa chỉ hoạt động trên trục bên phải.Thứ hai, và quan trọng nhất là tổng số địa chỉ bitcoin không chỉ cho thấy sự quan tâm dựa trên nhu cầu tổng thể, mà còn ẩn bên trong nó là tổng số lượng hodler tiềm năng. Thêm vào đó, thông tin về số lượng địa chỉ hoạt động không được tiết lộ, tức là có thể một số địa chỉ không hoạt động trong một thời gian rất dài nhưng vẫn đang giữ Bitcoin, do đó sẽ làm giảm tổng nguồn cung.
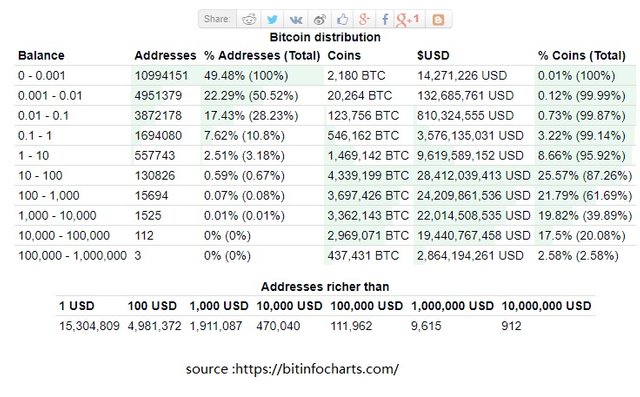
Tính đến ngày 15.06.2018, theo dữ liệu từ blockchain.info tổng số địa chỉ Bitcoin hoạt động là hơn 400.000, trong khi số địa chỉ thực sự giữ bitcoin đã vượt quá 22 triệu.Thứ ba, nếu xem xét toàn bộ hệ thống – tổng số địa chỉ Bitcoin vẫn có mối tương quan đáng kinh ngạc với giá bitcoin trong thời gian dài.
Mô hình tiếp theo sẽ được xây dựng xung quanh tổng số địa chỉ (chứa tất cả thông tin động về cung và cầu). Tôi đã lập mô hình nhật ký giá bitcoin là hàm bậc hai của tổng số địa chỉ. Trước tiên, chúng ta hãy xem xét mối quan hệ đầu tiên giữa từng cặp với nhau bao gồm: giá Bitcoin, các địa chỉ hoạt động và tổng số các địa chỉ. Giả thuyết đầu tiên là giá Bitcoin và với các địa chỉ hoạt động và sau đó là giá Bitcoin và tổng số địa chỉ.
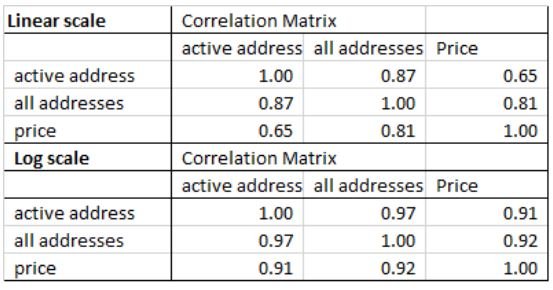
Tổng tương quan giữa địa chỉ hoạt động với tất cả các địa chỉ và giá
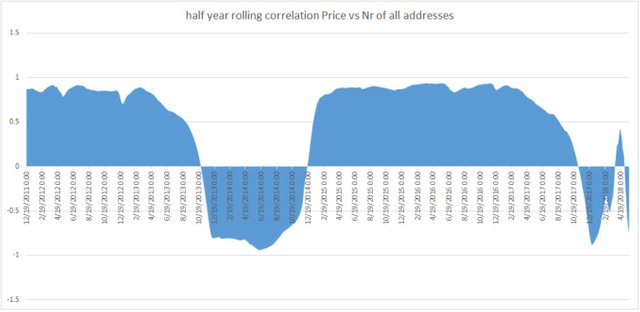
Hoạt động tương quan giữa giá và Nr của tất cả các địa chỉ, khi dịch chuyển từ gần như dương 1 (hoàn toàn tương quan) sang âm 1, mô hình cho thấy sẽ có một bong bóng sớm xuất hiện
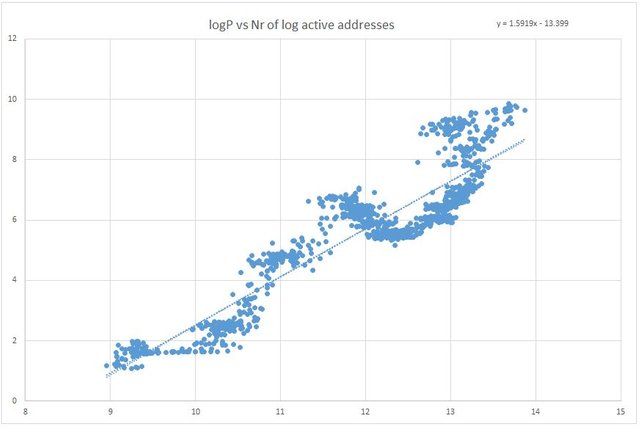
Tương quan tuyến tính giữa giá bitcoin với tổng số lượng địa chỉ đang hoạt động. Với trục Y là giá Bitcoin và trục X là số địa chỉ đang hoạt động (N).
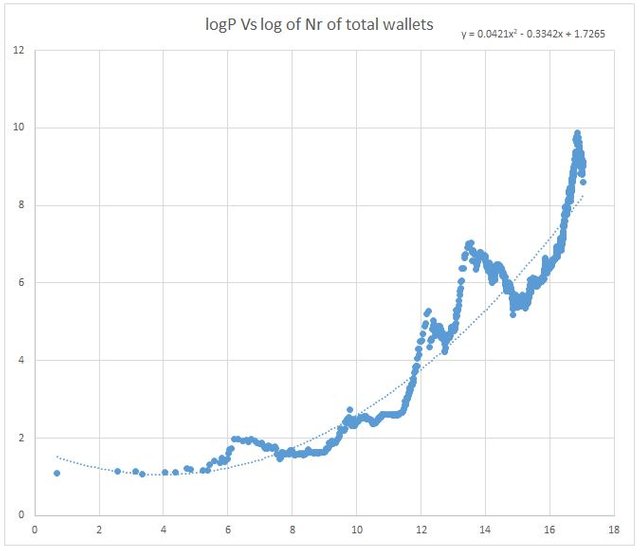
Biểu đồ cho thấy mối quan hệ đa thức giữa giá Bitcoin và tất cả các địa chỉ được tạo ra. Với trục Y là giá Bitcoin và trục X là số địa chỉ đang hoạt động (N).
Biểu đồ đầu tiên gần giống với biểu đồ được tạo ra bởi Wheatley, Spencer, và cộng sự (2018), nơi họ ước tính giá trị độ dốc vào khoảng 1,69, trong khi ước tính của chúng tôi là vào khoảng 1,59.
Biểu đồ thứ 02 cũng cho thấy mối quan hệ thú vị giữa các địa chỉ và giá cả, nhưng hiếm khi được nghiên cứu. Nó cho thấy có một mối quan hệ bậc hai giữa chúng.
Dựa trên các biểu đồ trên, mọi người có thể thấy rằng đợt tăng giá lần cuối cùng – vào cuối năm 2017 – giá đã vượt qua đường xu hướng đa thức trong giai đoạn 2013 – 2014, và cho thấy rằng hiện tại chúng ta đang ở giai đoạn tương tự như thời kỳ bong bóng từ 2013 – 2014.
Hiện tại, đây là thời điểm tốt nhất để bàn về định luật Metcalfe
Nói chung, định luật Metcalfe cho rằng giá trị của mạng lưới là hàm bậc hai đối với số người dùng đang hoạt động của mạng lưới đó. Trong các mạng lưới thuộc thị trường Crypto, địa chỉ hoạt động và tổng giá trị mạng lưới thường được sử dụng để kiểm tra định luật Metcalfe.
Nhưng về cơ bản, mạng lưới crypto rất khác biệt so với những mạng lưới khác. Tại một thời điểm nhất định, chỉ có một nguồn cung hữu hạn đang lưu thông trên thị trường. Chúng ta có thể áp dụng định luật Metcalfe nếu biết chính xác lượng cung đang hoạt động tại thời điểm thử nghiệm.
Tất cả các nghiên cứu đều lấy tổng giá trị mạng lưới, giá coin trong thời gian lưu thông. Và hầu như tất cả các nhà cung cấp dữ liệu đều tính tổng giá trị của mạng lưới theo cách đó.

Tuy nhiên, hiện tại, có khoảng 2,4 triệu Bitcoin đã không còn được lưu thông. Không ai biết chính xác được có bao nhiêu bitcoin bị mất vĩnh viễn, do đó việc sử dụng giá trị mạng lưới hiện tại làm giá trị đầu vào có thể dẫn đến một số sai sót và kết quả thu được sẽ không phản ánh mối quan hệ giữa số địa chỉ hoạt động và “tổng giá trị mạng lưới”.
Hiện tại tỷ lệ mất mát là đủ nhỏ để không gây ra bất kỳ sự bất thường đáng nào, tuy nhiên hãy tưởng tượng nếu mạng lưới chỉ còn 2,1 triệu BTC lưu thông thì sẽ như thế nào?
Nếu định luật Metcalfe là đúng và tổng số địa chỉ hoạt động vẫn ổn định, thì người ta có thể mong đợi tổng giá trị mạng lưới vẫn ở mức hiện tại. Và mọi người vẫn sẽ sử dụng số lượng lưu thông cũ để tính giá trị mạng lưới, đến kết quả sai. Điều này thật sự rất nguy hiểm vì hiện tại, vẫn còn rất nhiều trường hợp sử dụng định luật Melcalfe sai cách.
Trong thực tế, ngay cả những đồng tiền chỉ “tạm thời không lưu thông” sẽ vẫn có ảnh hưởng đến tổng giá trị mạng lưới crypto. Tiền mã hóa không chỉ phục vụ như một phương tiện trao đổi, mà còn là tài sản lưu trữ giá trị. Như vậy sẽ luôn có một số lượng coin nhất định đang không tham gia lưu thông, nhưng không mất đi và không ai biết chính xác con số này.
Do đó, định luật Metcalfe có thể tốt trong việc đánh giá tính thanh khoản của mạng lưới crypto, nhưng nó không để cập đến số coin đang được HODL hoặc đơn giản là mất đi.
Giả sử định luật Metcalfe thực sự coi trọng tính thanh khoản của mạng lưới, nếu nhu cầu sử dụng và số địa chỉ hoạt động vẫn ổn định, trong khi nguồn cung thấp hơn, giá của một Bitcoin sẽ tăng lên. Xem biểu đồ và chú thích bên dưới.
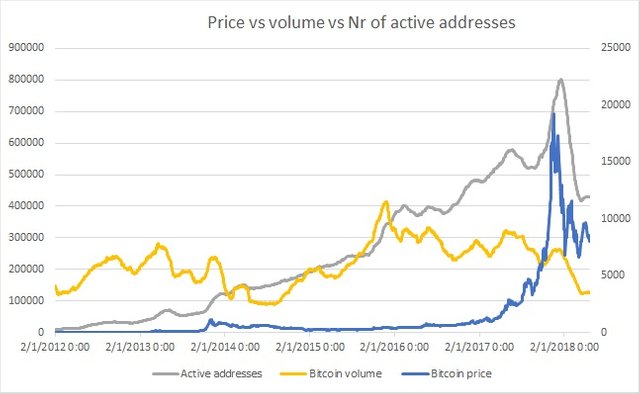
Số lượng địa chỉ hoạt động hiện tại tương tự như nửa đầu năm 2016 nhưng giá lại cao hơn rất nhiều, nếu định luật Metcalfe đúng, thì tổng số bitcoin hiện hành sẽ thấp hơn năm 2016, như đường màu vàng trên biểu đồ – khối lượng giao dịch bitcoin hàng ngày thấp hơn rất nhiều so với năm 2016, giá Bitcoin trên trục bên phải, địa chỉ và khối lượng được thể hiện trên bên trái.
Trong khi đó, không ai biết số tiền thực sự bị mất hoặc bị khóa bởi holder nên rất khó để kiểm tra lý thuyết này một cách chính xác hoàn toàn. Do đó thay vì thử nghiệm định luật Metcalfe với tổng giá trị mạng lưới. Tôi đề nghị sử dụng cách đo nguồn cung và cầu. Như đã đề xuất, tôi đề xuất giả thuyết mới nhằm nắm bắt cả giá trị mạng lưới – khi tài sản crypto được sử dụng làm phương tiện trao đổi và giá trị lưu trữ – nó được sử dụng làm phương tiện để lưu giữ giá trị.
Giá của tài sản crypto là một phương trình bậc hai của tổng số địa chỉ được tạo ra.
Lợi nhuận dự kiến và biến động, dự báo và mô phỏng
Tôi đã lập mô hình với giá và tổng số địa chỉ là đường cong tăng trưởng theo cấp số nhân, cho thấy một mối quan hệ thú vị giữa biến động và lợi nhuận của Bitcoin. Xem bên dưới.
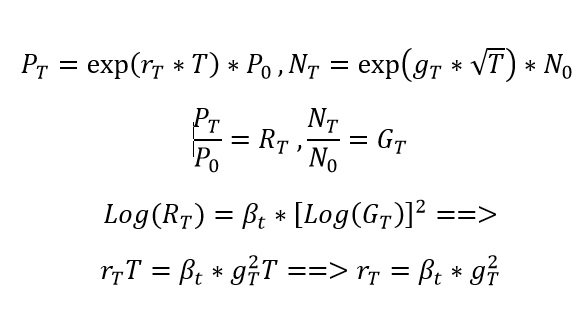
Giải thích về mô hình như sau: trong khi thông thường giá tỷ lệ thuận với bình phương tổng số địa chỉ được tạo ra, độ dốc là một biến theo thời gian, giai đoạn beta có thể được theo sau bởi các giai đoạn beta và vise -versa khác. Do đó nếu giá giảm, kèm theo đó là beta giảm, giá cuối cùng sẽ về mức 0.
Đây là một số quan sát khá thú vị.
Vì chúng ta chọn phương trình bậc, đầu tiên dR_T dùng để đo tốc độ thay đổi của R_T – lợi tức kỳ vọng của giá trong khoảng thời gian dT. Sau đó dd (R_T) là đại lượng dùng để đo lường tỷ lệ thay đổi của lợi tức. Và đây là công thức tính toán sự biến động.
Xem biểu đồ dưới đây, tôi sẽ tính toán beta bằng cách sử dụng giá sẵn có và số lượng tất cả các địa chỉ, đặt tên là “truebeta”, sau đó tôi sử dụng mô hình Generalized-Autoregressive-Score của Creal, et al. (2013) để ước tính biến động có điều kiện thay đổi theo thời gian T với 5 bậc tự do.
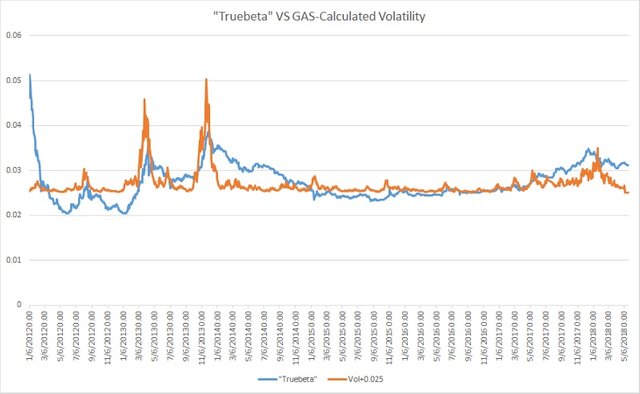
Ước tính biến động có điều kiện được tăng lên 0,025 để so sánh trực quan tốt hơn
Thiết kế mô hình của chúng tôi ở đây cũng đưa ra lời giải thích cho các quan sát được ghi nhận vào đầu năm 2013 bởi Bouri. E và cộng sự rằng những cú sốc tích cực sẽ làm tăng sự biến động có điều kiện nhiều hơn so với những cú sốc tiêu cực. Sau đó, tôi sẽ kết nối chúng với giả thuyết mà tôi đã đưa ra trong chương trước về sự thay đổi giữa cung và cầu, lợi nhuận kỳ vọng và biến động.
Nó thường được chấp nhận bởi các chuyên viên tài chính rằng lợi nhuận là ngẫu nhiên và không thể dự đoán được, biến động rủi ro của các lớp tài sản chỉ có thể dự đoán được ở một mức độ nào đó. Do đó thiết kế mô hình và giả thuyết vốn có về mạng lưới Bitcoin, giá bitcoin chỉ có thể dự đoán được tương đối so với các loại tài sản Delta khác và lợi nhuận kỳ vọng sẽ có sự tương quan với biến động.
Sự biến đổi sau đây được thực hiện để biến đổi mô hình phi tuyến tính thành mô hình tuyến tính (Lý do tôi làm điều này là để giúp đơn giản hóa việc tính toán, điều này không ảnh hưởng đến kết quả hồi quy). Có thể nhận ra rằng mô hình được biến đổi phù hợp với dạng state_space với log (beta) là nguồn duy nhất bị lỗi.
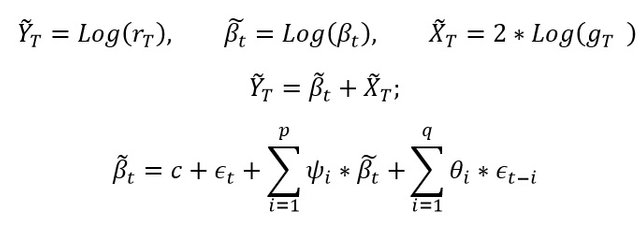
Tiếp theo, tôi đã chuyển đổi thủ công giữa các mức độ trễ cho đến khi tìm thấy mức phù hợp nhất, các thông số ước tính và t-stastic được liệt kê bên dưới. Được mã hóa và thử nghiệm trong MATLAB.
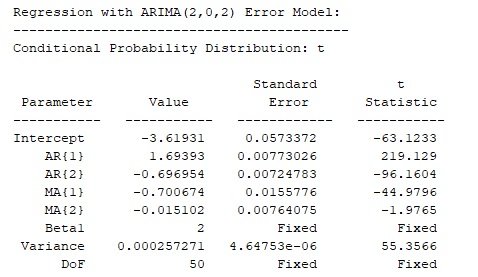
Tổng của các tham số AR gần với 1, điều này thường có nghĩa là mô hình được phân biệt, tôi đã thử thứ tự đầu tiên của quá trình đăng nhập (beta_t), tuy nhiên các mô hình này quá rộng lớn do đó tôi sẽ quay trở lại với mô hình ban đầu. Mặt khác, tổng các thông số AR cho biết tính bền vững của quá trình, tốc độ hồi phục của giá. Tổng có giá trị càng gần 1 thì có nghĩa là quá trình này rất bền bỉ và hồi phục rất chậm. Trong mô hình của chúng tôi cho thấy beta hình thành đà giá rất rõ ràng, có nghĩa là giá bitcoin rất có khả năng sẽ tăng hoặc giảm trong thời gian dài.
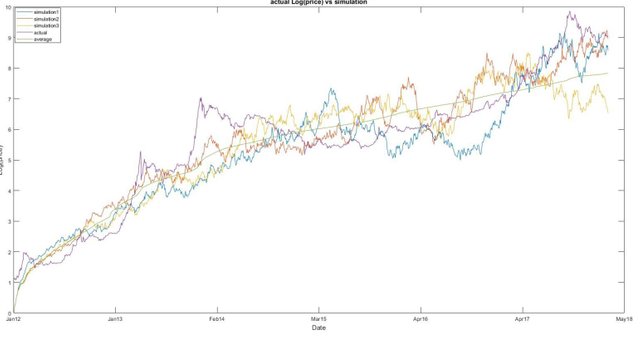
Sau đây tôi đã chạy 5000 mô phỏng trên Nr địa chỉ hiện tại và đã tìm ra 3 mô phỏng đầu tiên, có giá trị trung bình trên tất cả 5000 mô phỏng, cùng với giá bitcoin thực tế.
Như được thấy từ biểu đồ bên dưới giá thực tế và giá mô phỏng đã đan xen vào nhau, trung bình tính toán của 5000 mô phỏng đưa ra ước tính giá trung bình khoảng 7.8 vào ngày 22.05.2018, tương đương khoảng 2700 USD, chúng ta vẫn có thể có một thị trường “gấu” ở phía trước, được ghi nhận vào ngày 22.05.2018. Lưu ý rằng, nếu có sự thay đổi cơ bản đối với các loại tài sản, betas thực sự cũng sẽ thay đổi cùng với nó, do đó tốt nhất là kết hợp các nguyên tắc cơ bản cùng với các kỹ thuật thống kê khi ước tính giá trị của chúng trong tương lai.
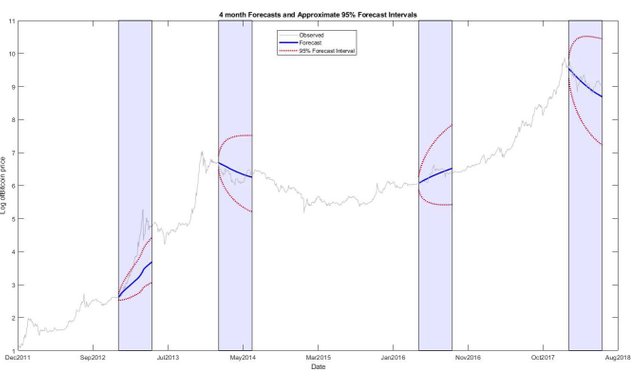
Tiếp theo, tôi đã kiểm tra độ chính xác của dự báo bằng cách chọn tùy ý 04 khoảng thời gian (mỗi khoảng có độ dài 04 tháng) trong 6 năm vừa qua và sử dụng thông số ước tính cũng như thông tin mới nhất về giá và địa chỉ để đưa ra giá cả dự báo. Trong số 4 khoảng thời gian này, mô hình thành công dự đoán xu hướng 4/4 lần, với độ tin cậy khoảng 95%, thời điểm duy nhất giá rơi ra khỏi vùng tin cậy là vào đầu năm 2013, khi giá đã trải qua thời kì tăng trưởng hyperbolic.
Cho đến nay có vẻ như mô hình có thể nắm bắt đầy đủ các động lực giá của các loại tài sản crypto, và mọi người có thể áp dụng chúng cho mô phỏng trong tương lai.
Như đã nói ở trên, tôi đã mô hình hóa giá bitcoin với tốc độ tăng trưởng liên tục g lần sqrt (T), quỹ đạo tăng trưởng địa chỉ bitcoin cũng có sự di chuyển thích hợp trong mô hình này. Có thể có sự thay đổi cơ bản trong giai đoạn phát triển Bitcoin sau này sẽ khiến nó cần một mô hình giá mới.
Sau đó, chúng tôi cũng muốn đưa ra dự báo giá dựa trên số lượng địa chỉ được thống kê trong 03 năm tới.
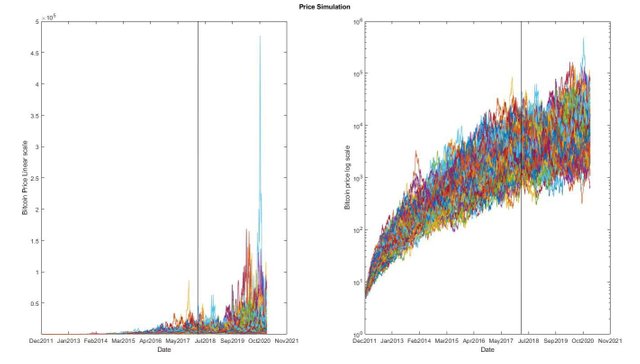
Tôi mô phỏng thêm 5000 đường giá trên tổng số địa chỉ ước tính. Con số dưới đây cho thấy sự so sánh giữa giá bitcoin trên thang đo tuyến tính so với giá trên thang log trong 100 mô phỏng đầu tiên. Trái ngược với nghiên cứu của Wheatley, Spencer và cộng sự (2018), tài liệu cho rằng bong bóng có thể phát hiện được, mô phỏng tỷ lệ tuyến tính dưới đây cung cấp một quan niệm khác, thị trường bong bóng hiện tại sẽ xuất hiện một cách ngẫu nhiên và rất khó lường trước.
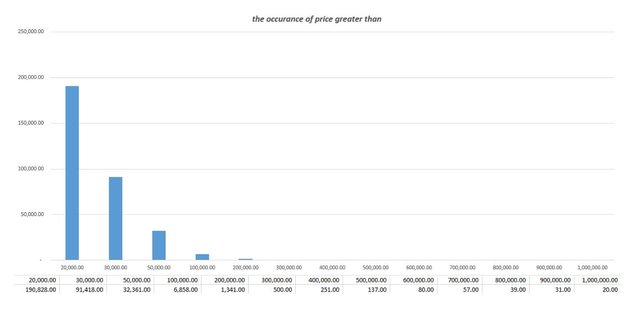
Nhìn từ góc độ khác, trong số 5000 đường giá này, có 20 ngày mà giá của một bitcoin kết thúc trên 1 triệu USD, 6858 ngày vượt quá mức 100.000 USD. Và rất nhiều ngày giá bitcoin trên mức 20.000 USD.
Số liệu trong hình bên dưới cho thấy tổng số thời điểm mà giá Bitcoin sẽ vượt qua một mốc cố định nào đó trong tương lai. Số liệu này chỉ mang tính chất tương đối và tham khảo. Tuy nhiên nó cho thấy giá Bitcoin sẽ có xu hướng tăng trong những năm sắp tới.
Kết luận
Tôi tin rằng bài viết này cung cấp một khuôn khổ định lượng đơn giản để dự báo giá, và càng mở rộng từ bitcoin sang các loại tài sản khác.
Do đó bằng cách mở rộng, mọi người có thể dự đoán tổng số địa chỉ có thể tăng nhanh đến mức nào, đồng thời ước tính mức giá của tài sản crypto trong ngắn hạn.
Tôi chắc chắn rằng hầu hết mọi người sẽ đồng ý với tôi rằng một số yếu tố, ví dụ như nhà sáng lập, sức mạnh của đội ngũ, lợi ích mang lại cho cộng đồng, tình cảm thị trường… là những yếu tố rất quan trọng đối với dự án. Những yếu tố này trực tiếp ảnh hưởng đến số lượng địa chỉ phát triển. Dựa trên điều này các nhà quản lý quỹ sẽ có thể xây dựng mô hình định giá và rủi ro tùy chỉnh cho riêng mình.
Đề xuất sửa đổi luật của Metcalfe cũng được thảo luận chi tiết và trong kiến thức hạn chế của tôi, đây là lần đầu tiên điều này được thảo luận đến.
So với tài sản truyền thống, biến động có điều kiện của thị trường này sẽ đảo ngược. Đây là một quan sát rất quan trọng đối với các nhà giao dịch tùy chọn crypto. Khi hiệu chuẩn biến động sẽ được đảo ngược về mặt lý thuyết.

Hạn chế:
Trước hết, sự mô phỏng dựa trên giả định rằng sẽ luôn có người sử dụng mạng lưới, nếu một mạng lưới không có người sử dụng thì giá trị của nó sẽ về 0. Tôi đồng ý về điểm này và thừa nhận phương pháp của tôi chỉ có thể tốt cho việc mô phỏng giá trong thời gian trung và ngắn hạn.
Ngoài ra, khung tính toán và mô hình có thể cần được cải thiện
Thứ ba, tôi bỏ qua mối tương quan giữa tốc độ tăng trưởng địa chỉ và beta, và mô hình hóa mỗi thứ như thể chúng độc lập với nhau, điều này rõ ràng là không đúng sự thật kể từ khi dữ liệu thực nghiệm cho thấy rằng betas có tương quan với vận tốc tăng trưởng của số lượng địa chỉ.
Cuối cùng, mô hình yêu cầu nhiều dữ liệu trong lịch sử và chỉ có thể được áp dụng riêng lẻ vì các dự án khác nhau sẽ có đường cong beta rất khác nhau. Tôi đã không tiến hành kiểm tra các loại tài sản khác ngoài Bitcoin.
Cuối cùng nhưng không kém phần quan trọng, khi tôi không giải thích được mối tương quan giữa sự tăng trưởng địa chỉ và beta, đó sẽ là tâm điểm của nghiên cứu trong tương lai của tôi. Tôi tin rằng ẩn bên trong nó là câu trả lời cho sự biến động và lợi nhuận trong tương lai. Đối với bitcoin, cũng như các tài sản crypto khác, nếu việc chấp nhận hàng loạt xảy ra, tôi nghi ngờ sự biến động cũng như lợi nhuận kỳ vọng sẽ tương tự với tiền pháp định, do đó “tiền xu ổn định” trong thời gian dài chỉ là tạm thời giải pháp và không thực sự cần thiết. Ý tưởng này được lấy cảm hứng từ nghiên cứu của Catalini và cộng sự (2018) về việc giá trị crypto sẽ phát triển như thế nào, cũng như các cuộc thảo luận mà tôi đã thấy trên Twitter. Kết quả này có thể hữu ích cho các công ty khởi nghiệp crypto, theo cách mà họ không còn cần phải thuê “các nhà sản xuất thị trường” để thao túng giá cả. Họ chỉ cần tập trung vào sản phẩm và thị trường sẽ xử lý phần còn lại.
Tham khảo :
- Athey, S., Parashkevov, I., Sarukkai, V., and Xia, J. (2016), “Bitcoin pricing, adoption, and usage: Theory and evidence,” mimeo., Stanford.
- Bouri, E., Azzi, G., & Dyhrberg, A. H. (2016). On the return-volatility relationship in the Bitcoin market around the price crash of 2013.
- Catalini, C., & Gans, J. S. (2018). Initial coin offerings and the value of crypto tokens (No. w24418). National Bureau of Economic Research.
- Creal, D., Koopman, S. J., & Lucas, A. (2013). Generalized autoregressive score models with applications. Journal of Applied Econometrics, 28(5), 777–795.
- Wheatley, Spencer, et al.(2018) “Are Bitcoin Bubbles Predictable? Combining a Generalized Metcalfe’s Law and the LPPLS Model.” .
Nội dung trong bài viết có thể bao gồm ý kiến cá nhân của tác giả và tùy thuộc vào điều kiện thị trường. Mọi người nên thực hiện nghiên cứu thị trường của riêng mình trước khi đầu tư vào tiền mã hóa. Pink Blockchain cũng như tác giả sẽ không chịu trách nhiệm về mọi tổn thất tài chính của bạn.
Link bài gốc: https://pinkblockchain.com/mo-hinh-dinh-gia-bitcoin-dinh-luat-metcalfe-bien-dong-va-mo-phong-tuong-lai/