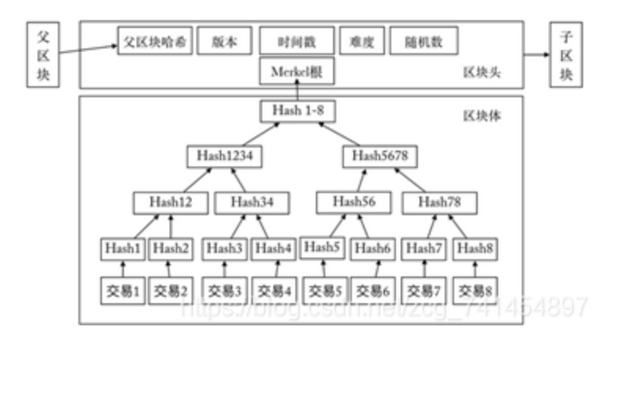
Let me first introduce the data structure of each block of Bitcoin. Each block is composed of a block header and a block body.
The block body contains several transaction information collected by miners. In the figure, it is assumed that 8 transactions are included in the block. All transactions generate a Merkel tree. The Merkel tree is a data structure. The leaf nodes are hashed in pairs to generate the upper layer of nodes, and the upper nodes are hashed to generate the upper layer, until finally a tree root is generated, called the Merkel tree root, and only the tree root remains in the block header. It can save the space of the block header and facilitate transaction verification.
The block header contains the hash of the parent block, version number, current timestamp, difficulty value, random number, and the Merkel tree root mentioned above.
Assuming that the blockchain has been linked to a certain block, four ABCD nodes have collected some transaction information in the entire network in the first ten minutes. They selected about 4k transactions among them, packaged them, and generated the Merkel tree root. Combine the information in the block header, that is, block hash + version number + timestamp + difficulty value + random number + Merkel tree root to form a string str, and a binary number of 256 is obtained through two hash functions , That is, SHA256(SHA256(str)) = 10010011...a total of 256 bits, Bitcoin requires, the generated result, the first n bits must be 0, n is the difficulty value, if the binary number generated now does not meet the requirements, it must be changed The value of the random number is recalculated until the result that satisfies the condition is calculated. Assuming that n is 5, the generated binary number must be 00000... (256 bits in total). Once mining is successful, miners can broadcast this message to the entire network, and other miners will continue mining based on the block. The hash value of the parent block in the next block header is 00000...this number generated by the previous block.
Solving this mathematical problem depends on luck. In theory, the most lucky miner may be able to calculate the result with one hash, while the one with poor luck may never be calculated. But on the whole, if a miner's computing power is greater, the number of hashes per unit time is greater, and the more likely it is to succeed in mining in a short time.
So how is n determined? Bitcoin designers hope that on average, a block will be generated every ten minutes. On the whole, the probability of successful mining is 1/2^n. Now suppose there are 1W mining machines in the world, and the computing power of each mining machine is 14T times/s = 1.4×10^13 times/s. The unit time/s is called the hash rate. 10 minutes is 600s, so 10 You can do 8×10^19 hash operations in a minute. From a probability point of view, you need to do 2^n operations to succeed in mining. You can list the equation 2^n = 8×10^19, and you can solve for n It's about 66. So with this method, we have no way to make our luck better, we can only improve our computing power and calculate the result as soon as possible.
In addition, the C++ code that needs to simulate the mining process can reply to the mailbox. The code can simulate the mining algorithm of Bitcoin by adjusting the difficulty value to control the speed of block generation.