如今,大段地抄袭的剽窃者减少,新的剽窃模式是偷窃他人的概念与创意,改写变成自己的成果并抢先发布,即使被发现,狡辩为巧合。很多发生在审稿过程中,严重侵犯作者的权益,败坏学术环境。杂志社不公开审稿人身份,起到了保护学术窃贼的作用,学术管理机构处理的难度加大,学术偷窃成功率很高,成本很低。 C.Devon Lin 等加拿大SFU博士的论文具有这种特征。他们的论文与我的当时正在接受审查的稿件如此系统地相似,疑似他们从我的稿件的审稿人那里偷窃我的系统设计和创新元素,加以改写,抢先宣读,占住首发位置,然后释放我的稿件。遗憾的是,几乎所有偷窃改写的内容都发生了严重的错误,除了只用“ get"一词省略了交换算法推导过程之外。有关真相披露于此,请公明鉴。
3. 系统模仿与基本概念定义造假
3.1 He(2009)的基本定义
遵循一般的数学方法,He(2009)首先定义基本概念 零相关设计 和 弱相关设计,然后研究零相关设计的存在性和多解性, 以最大相关系数的绝对值 (mcc) 为优化目标,从基本向量置换集中反复随机抽样,选择被抽选向量的分量进行交换实现 mcc 的极小化, 如果 mcc 不能极小化到 0,则得到近似解弱相关设计,最后研究零相关设计的性质和数据处理方法。基本概念的定义截图如下:

3.2 正交拉丁超立方的文献定义
在拉丁(离散)空间中,McKay, Beckman, 和 Conover (1979) 用相等的边际概率(1/n) 将每个xk 的范围划分为n 层,每层采样一次,定义了拉丁超立方采样(LHS): Ye(1998), Steinberg 和 Lin(2006) 用每个变量 xk 的水平等距离定义拉丁超立方设计(LHD), 用满足条件:
的 LHD 定义正交拉丁超立方设计(OLHD)。ye(1998) 的定义具有一般性。等距离意味着该距离可以是 1,也可以不是 1,也可以不是整数,中点可以在 0,也可以不在 0。 Steinberg and Lin(2006) 构造的一个有名的 OLHD,其水平间距离就不是 1,Mckay 的 LHS 是小数。
3.3 Lin(2008)的基本定义
Lin 研究 OLHD,给拉丁符号赋予数值属性,给拉丁向量赋予均值、方差、内积和相关系数等数字特征, 把拉丁空间变成了实欧氏空间,其 LHD 定义如截图(红色标记为本文作者所加,下同)。
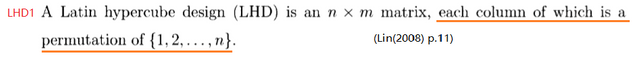

作者谬矣,零相关的不一定是正交的,不能用零相关定义 OLHD。 零相关的LHD只能定义零相关设计, 这恰恰是He(2009) 的论题,作者强迫零相关设计戴上 OLHD 帽子而已。这是模仿 He(2009) 的铁证。 Lin(2008)为什么不遵循文献定义,奥秘在于她要模仿He(2009) 的零相关矩阵的存在性定理。不幸的是,当她着手证明该定理时发现,所有 LHD1 不正交,OLHD 不存在,存在性定理不成立,其定理 2.5 的必要性部分不能被证明。 在该定义下,Lin 的堆叠法无效,她的定理 2.5 的充分性部分也不能被证明。 她这才不得不紧急地定义第二个LHD。

这样,在相邻两段文字中定义了两个 LHD。 它们不是 Lin 说的稍微不同,而是典型的二义性定义。作者反复变换LHD的概念定义为的是让 LHD 概念定义适合存在性定理。其结果致使文献上的一些有名的结果都排除在他们的 LHD 范畴之外。 Steinberg and Lin(2006) 构造的一个有名的含有12正交列的16运行 OLHD,其水平间距不是 1, Mckay 的 LHS 的间距是小数(概率),Ye(1998) 的 LHD 中点不在 0。 特别地,Lin 的 LHD 的线性变换的结果不在自己的 LHD 范畴之内。
他们总算拼出了存在性定理的一个证明,但他们没有就一般 LHD 证明存在性定理。得意忘形居然忘记了用正交性定义(3.1) 修改他们的定义 2.1 ,留下了偷窃的证据。
3. 4 Nearly Orthogonal 是个什么统计学概念
作者给拉丁符号赋予数值属性,给拉丁向量赋予均值、方差、内积和相关系数等数字特征, 但作者定义的 correlation 与自由度无关,不使用相关性临界值,不定义相关性置信概率, 凡是不正交的都是 nearly orthogonal。这是不正确的。 相关性应该有临界值(门槛),这个临界值应该是相关性置信概率与自由度的二元非线性函数。 任何统计结果都应该符合统计学原理,接受统计检验。 当涉及到人的安全性时,更应该慎重,提高统计学门槛。 那种除了犯罪的就都是 nearly 犯罪的命题是不能接受的。
在 Lin(2008) p.19, Lin(2010) p.5 中有一个扩充有名的 Steinberg and Lin(2006) 构造的 OLHD,它的相关矩阵如下图 (为节省篇幅,只显示局部)。

其中有四个子设计的最大相关性置信概率大于 0.99 甚至是 1,如何界定它是或不是 “a nearly orthogonal design”?相关性从 0 到 1 的范围可以划分为若干段,根据工程需要,确定临界值以定义弱相关门槛来界定弱相关设计范畴是唯一的解决办法。于是,她写了一个有失基本逻辑的定义。

column-orthogonality 比 orthogonality 弱如何理解,“each column of D to be balanced” 是什么意思?它与该设计的正交性之间有什么关系? 事实是即使设计的边际分布都是均匀的,联合分布可以是完全相关的。 句中有一个词 “weaker” ,表明作者想定义弱相关设计。但是作者不定义弱相关设计,不知作者之所云。但是作者明明白白地构造了一组弱相关阵列,Lin(2008) 的表 2.3-2.4 与~He(2009) 的结果完全相同。 既然不定义临界值,不定义弱相关性,非正交都是 nearly orthogonal,构造这些矩阵干什么? 它证明作者偷了He(2009) 的概念用了不敢公开。
He(2009) 定义并构造的弱相关设计具有三个特征:
- 包含一个零相关子阵,如果它存在;
- 设计的相关性总体上比较弱;
- 随列数增加,子阵的 mcc 以及相关性置信概率最大值 Pmax 递增不减。
不知道在我之前谁定义并构造过这样的设计,我在2005-2006 年间构造了运行数范围在4-33 之间的 第一版弱相关超立方表 于2011 年3月29日发布我的网站上。现取出 16 运行W16h5o(2006年6月10 日构造) 与作者文中的相应结果比较相似性。小规模弱相关设计在《弱相关试验设计》中可以找到。
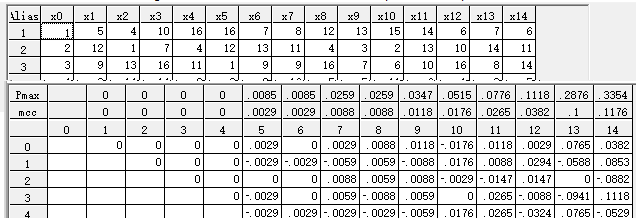
下边的一个来自 Lin 的两篇论文 (Lin(2008)p.27, Lin(2010)p.14)。
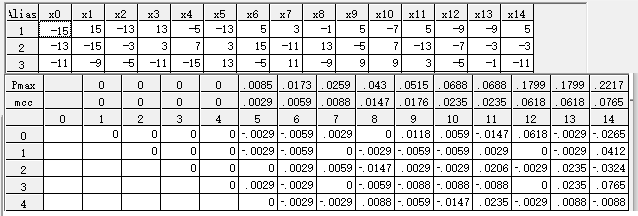
这两个结果本质上完全相同。