
Overview
When the distributed nodes in a blockchain network communicate and interact, it is necessary to rely on a digital signature technology to confirm the identity and verify the authenticity, integrity and non-repudiation of the information to achieve mutual trust. The role of digital signatures is to:
(1) verify the identity of the sender of the message, and
(2) verify the integrity of the verification message.
The principle of a digital signature is that the signer uses his own private key “sk” to sign the message M, obtain the signature result S, and then send the signature S together with the message M. The recipient verifies the signer’s signature using the signer’s public key “pk”.
After an in-depth analysis of various mainstream digital signature schemes, the Penta team built and implemented the Penta digital signature scheme based on its uniquely designed account model and actual business scenarios. This is described in detail below.
Asymmetric algorithm
In the asymmetric algorithm, each communicating party uses a public-private key pair (pk, sk), wherein the private key “sk” is stored in its own secret, and the public key “pk” is public. Asymmetric algorithms mainly have two applications:
(1) encryption scheme: encrypt the message with the public key, and then decrypt the message with the private key;
(2) signature: use the private key to sign the message, and then use the public key to verifies the signature.
Commonly used asymmetric algorithms are:
(1) RSA algorithm
The RSA algorithm was jointly proposed by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977 and is currently widely used in encryption. The security of the RSA algorithm is based on the problem of large integer difficulty decomposition. Given that two large prime numbers p and q are easily multiplied to obtain n, it is extremely difficult to factorize n.
(2) ECC algorithm
ECC (Elliptic Curve Cryptography) is an elliptic curve cryptography algorithm, which defines an elliptic curve y²=x³+ax+b(mod p) on a finite field. The values of a, b, p must satisfy certain construction conditions. Thereby an elliptic curve based on different parameters is formed. The security of the elliptic curve cryptosystem is based on the difficulty of the elliptic curve discrete logarithm problem (ECDLP). So far there is no effective cracking method.
Compared with RSA, ECC has absolute advantages in many aspects, such as more attack-resistant, less calculation, faster processing, smaller storage space and lower bandwidth requirements. Therefore, the ECC algorithm is more used in the underlying blockchain technology.
ECDSA signature algorithm
The full name of ECDSA is Elliptic Curve Digital Signature Algorithm, which is an elliptic curve digital signature algorithm. The signature process is as follows:

In view of the good public key algorithm characteristics of ECC algorithm, Bitcoin uses ECDSA based on the elliptic curve of secp256k1 as its digital signature algorithm, and Ethereum also uses this scheme. It is worth noting that ECDSA is a non-deterministic signature algorithm. Because of the existence of the random number k, the signature generated by the same person each time is different for the same message. From a functional point of view, the signature function produces different outputs for the same input because the random number is mixed into the signature function.
Penta’s signature scheme
Since the Bitcoin UTXO model and the Ethereum account model are relatively simple, and the signed messages are mostly ordinary transactions, the non-deterministic ECDSA algorithm is well qualified for signature and verification. However, Penta has designed the “security private key”, “transaction private key”, “consensus private key” and “seed private key” in the account model for improving the overall security of the system. Therefore, it cannot completely follow the traditional Blockchain signature algorithm. According to the analysis, the messages related to the secure private key, the transaction private key and the consensus private key can be regarded as ordinary transactions, so that the ECDSA algorithm can be safely used. However, according to the design of Penta random algorithm in the DSC consensus, the value of the “seed private key” signature will be used as a new random seed to determine the next round of the block after hashing. If the non-deterministic ECDSA algorithm is used, it will cause a so-called stake grinding issue that current block producer tends to generate multiple results by repeated signatures, and finally selects a certain signature message that is beneficial to the next block generation and broadcasts to the entire network, so that the random seed of the random algorithm can be manipulated, thereby affecting the randomness, fairness and security of the blockchain network. So, for the signature of the seed private key, a deterministic signature scheme is needed to make it non-manipulable. The Penta team selected a more advanced and mature BLS signature scheme through in-depth research and repeated verification.
The BLS signature scheme was proposed by Boneh, Lynn and Shacham in 2003. The signature scheme generated by the signature scheme is very short and is often referred to as the short signature scheme. The signature of the scheme is an element on the elliptic curve group, and the verification algorithm uses a bilinear pairing. The scheme is a signature scheme based on bilinear pairing with unique determinism. The BLS signature scheme mainly includes the following four algorithms: (Setup, KeyGen, Sign, Verify)

The elliptic curves currently used to implement bilinear pairing are mainly divided into the following two categories according to the parameter settings:
(1) BN (Barreto-Naehrig) curve: A cluster of elliptic curves that are easy to do bilinear pairing. According to the length of the signature, it can be divided into BN-254, BN-381, BN-512 and so on.
(2) BLS (Barreto-Lynn-Scott) curve: A cluster of slightly older Pairing-friendly elliptic curves representing the curve BLS12–381.
Both Zcash and Dfinity projects currently use the BN-254 curve, but recent studies have demonstrated that the curve security level can only provide a 110-bit security. The BN-381 and BLS12–381 curves both provide 128-bit security which are 16% safer. While the BN-512’s security level is higher, but the resulting system throughput is reduced and additional Data storage overhead. Since 128 bits have been guaranteed to be sufficiently secure in practical applications, the Penta team chose BLS12–381, which is more mature in technology implementation, more complete, and more widely used, for seed private key signature.
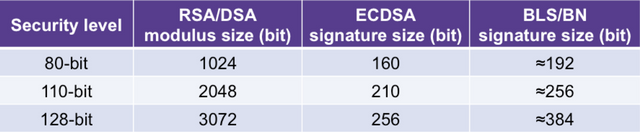
Comparison of security level and signature length of various signature schemes
Conclusion
In this paper, we introduce the algorithm related technologies including the ECDSA and BLS signature algorithms involved in the Penta project. The security of the blockchain itself is inseparable from the reliability of the digital signature technology. In the future, the Penta team will continue to conduct in-depth research based on the most advanced signature algorithms and continue to innovate and improve based on the actual application scenarios of the project, and promote the continuous iteration of blockchain digital signature and blockchain security technology.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://medium.com/@pentagf/introduction-to-penta-digital-signature-scheme-da216fbdb9ee
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yes, that's the original link
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit