AGRICULTURAL POLICY – COBWEB MODEL
BY: EDE KENNETH .K.
Agricultural goods are subject to variations in production for a variety of natural reasons. Excess rainfall, drought, pests and disease occur sporadically to cause differences between the planned output and that actually harvested or produced. Now, the demand for foodstuff is typically inelastic, so that shortages will force up prices considerably and gluts will produce very low prices. If the elasticity of demand is – 0.25, for example, then when production falls by 10%, prices rise by 40%. This inherent instability has given rise to a history of government intervention in agricultural markets.
The objectives of such intervention have varied from time to time but two of the most popular advocated have been to stabilize either food prices or farmers’ income. Assuming the demand curve is relatively stable, price and income fluctuations will be caused by supply fluctuations. A simple way for the government to keep food prices constant would be for them to establish a “Buffer Stock”. Then in the time of scarcity when the shortage would have caused prices to rise the government releases sufficient stocks to keep the market price constant. In years of bumper crops, when the excess supply would have reduced prices considerably, the government adds to its stocks, again so as to maintain constant market prices.
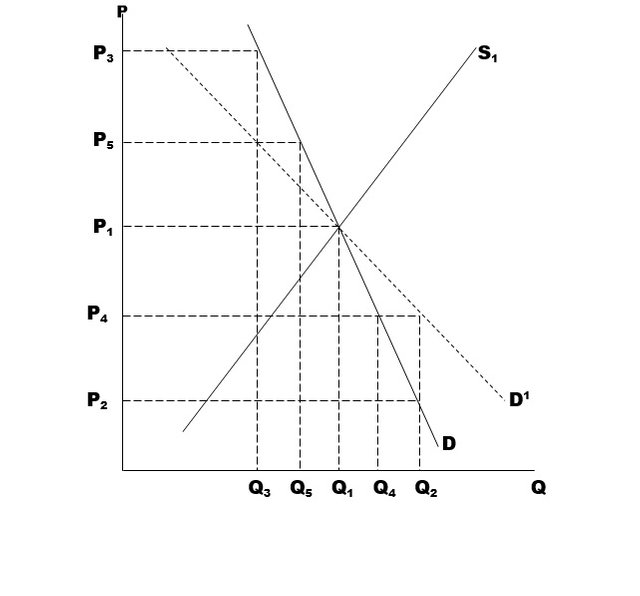
Fig. below shows the level of planned output for each market price. D is the relatively inelastic market demand curve. P1 and Q1 represent the average market price and quantity sold respectively. When the actual output increases say to Q2 the government buys (Q2 – Q1) to add to its stocks. When output falls below average, say to Q3 then the government releases (Q1 – Q3) to be sold on the market.
This policy stabilizes farm prices completely at P1 and given this would have been the average equilibrium price, the government can successfully operate this system indefinitely, provided it is prepared to subsidize the scheme to the extent of covering the costs to storage, which are not recovered elsewhere.
The effect of such a price stabilization policy on farmers’ income may be seen as follows: whatever the level of current output, the farmers either sell it on the market at price P1, or the government buys it to add to the buffer stocks, again at a price P1, i.e. the farmers face a perfectly elastic demand curve at a price P1. Thus, their income which is the total revenue (P x Q) they earn on the output they sell is directly proportional to the current output level. In poor years, their income will be low (as output is low), in good years, their output will be high (as output is high). Note that this effect on farmers’ income is the opposite of what would happen if the government had not intervened.
In order to stabilize farmers’ incomes, the government should stabilize their total revenue. If the farmers faced a demand curve for their product which was unitary elastic then their total revenue would be constant as the effect on revenue of quantity changes would be offset by compensating price changes. As we have said that market demand curve for agricultural goods is typically inelastic.
If the government chose to stabilize farmers’ income at their average level, i.e. at TR = P1Q1 in the fig above, then when fluctuation in output occur they must allow the market price to vary in the opposite direction by the same percentage amount, by adding or subtracting from their buffer stocks. Thus the actual demand curve facing producers D’ is unitary elastic and differs from the market demand curve D by the extent of government purchases or sales (the horizontal difference between D’ and D).
To maintain farmers’ income constant, when production falls to Q3 we require a price P5 (since P1Q1 = P5Q3 as both points lie on the same unitary elastic demand curve). At a price P5, the market demand exceeds the producers’ output by an amount (Q5 – Q3), which the government must release from its buffer stock.
Stabilizing farmers’ incomes in this way reduce fluctuations in prices which would be observed in free markets and also may show an operating surplus. The government would add to its stocks when prices are low, and sell from them when prices are high. If storage costs are not excessive, this scheme will be profitable.