May I start with a small introduction about the ideas that Platonism imposes for the readers which have not been familiar with the notion of Platonism , in general Platonism says that abstract objects like for example : a triangle , a point , a plane , a mathematical set etc , do actually exist in a objective sense ( these notions exist in the real world ) where as through this story I am going to refer as Non-Platonism to the complete opposite idea that these concepts are purely a product of the human mind in an attempt to approximate the world around and to model it and formalize it as much as we can . The purpose of this story is to share with you my personal thoughts on this matter and to actually create a discussion with the steemit fellows who are interested in these kind of questions .
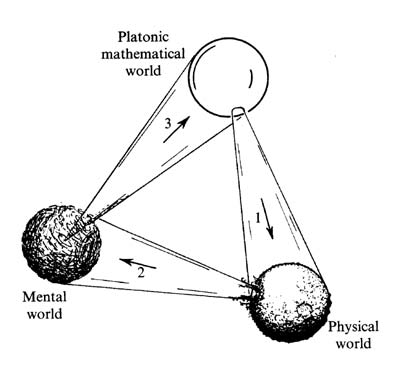
Personal opinion : My personal opinion is actually more oriented at the Non-Platonism idea and the reason behind this is the way we construct mathematical truth and truth in general , because in Platonism we kind of have the idealistic view for the abstract objects which we consider as being basic notions or we define them through out what we call a theory , and because at the same time looking at what we call axiomatic systems ( which is a set of statements that we agree that are true without the need of argument or in a sense we all can agree is intuitively trivial ) I get a kind of fuzzy feeling about Platonism , because it is at the base of mathematical truth that we can be as flexible as we want , for example , there is an axiom in Euclidian geometry which says : Given a geometrical line and a point say A which does not lie on this line , there is one and only one line that goes through that point and is parallel to the given first line , now consider if instead of this statement we would add something like : Given a geometrical line and a point say A which does not lie on this line , there are at least two lines that go through that point and are parallel to the given first line , this actually builds a whole new geometry which is called hyperbolic geometry (or Lobachevskian geometry) , but this is just an example , what is truly of importance is the fact that you can do this to any axiom which means that we can easily take the negation (the logical complement of what a statement says ) of every axiom in every axiomatic system and basically we can construct a true mathematical theory using that axiomatic system because that's the way we define truth to begin with , but of course axioms are statements which are build upon the abstract objects , but considering different axiomatic statements (where there are at least two axioms which represent the logical complement of each other ) we can easily conclude that those abstract objects behave in a complete different way in these kind of theories which have contradictory axioms , but of course they both speak about truths , truths which have place in our universe too because in our universe there are places where we have to use Euclidian geometry and there are places where we have to use Hyperbolic geometry , that kind of makes me feel like humans defined what truth is regarding their empirical arguments and as such they kind of forged axioms and abstract objects to fit the system then formalized it and attached symbols to those objects in order to create a deeper and wider view of the truth it can provide for us and in the end approximate real problems using those tools build upon those systems .
Anyways this is just an opinion and I am really open to a discussion with anyone who disagrees with me or agrees with me but wants to add something . I am waiting to hear from you
:)