Werner Heisenberg [1] actually called it the 'Indeterminacy Relation', but we usually call it the 'Uncertainty Principle'. It's something that a lot of nonsense is talked about, and I'll rant a little bit about that later on, but the key concept is that we cannot know certain combinations of things about the physical world to a precision greater than a particular limit.
Or can we? This post is an exploration of a set of experiments that seem to 'cheat' the Uncertainty Principle and allow us to know more than we theoretically should be 'allowed' to know about their characteristics. These experiments fall under the heading of 'weak measurement'.

Werner Heisenberg
Image credit: http://spaceandmotion.com/
The Uncertainty Principle
We most commonly think about it in the context of the momentum (or velocity, since the mass stays constant (except in relativistic contexts, but we won't get into that here!)) and position of a particle, but in fact the Uncertainty Principle applies to a range of sets of pair physical qualities of objects.
The relation can be written as follows, for the momentum, p, and position, x, of a particle such as a photon or electron:
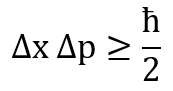
(A small physics refresher: the momentum is p=mv, the product of an object's mass and velocity.)
In fact, the relation also applies for a particle such as an elephant, but given its mass the uncertainty becomes vanishingly small for objects larger than an electron or a very small atom.
The Greek letter 'Δ' means 'the uncertainty in the measurement of', and the reduced Planck constant, ħ = 1.0545 × 10^−34 Js.
When we're talking about particles like a photon, which has no rest mass but has a momentum when traveling at the speed of light, or the electron with a rest mass of 9.1 x 10^-31 kg, this uncertainty can be considerable. For objects with larger masses the uncertainty becomes negligible. This is one of the reasons why the behaviour of the quantum world is so different from that of the 'classical' world that we all live in at our particular scale.
Note two things:
- The sign is '≥', which means that the product of the uncertainties can be greater, or it can be equal, but it can never be less than ħ/2. There is a lower limit on the uncertainties, and therefore a limit on the level of precision that we can attain.
- It is the product of the uncertainties in the measurements of the two quantities that is important, so if one decreases, the other must increase, and vice versa, to keep the answer the same.
It is important to note that this limitation is not a limitation or our instruments, or the experiments we can devise. From every experiment we have been able to do, it seems to be a fundamental feature of the universe.
Woo
Various practitioners of 'spiritual' and pseudoscientific 'woo' have latched onto the Uncertainty Principle as a way of saying "Everything is uncertain, man, and you can never know things precisely, so therefore my crystal healing and past life regression is every bit as valid as your science..." or words to that effect. This is nonsense. Have another look at that equation (technically I guess it's partway between an equation and an inequality) above, and at the size of the reduced Planck constant. The Uncertainty Principle does not mean 'everything is uncertain, nothing is certain'. It means that there are very tight, very tiny limits on the precision with which some specific measurements at the quantum scale can be made. At the classical scale, where we measure the velocity of a motorcycle - or the efficacy of crystal healing - the Uncertainty Principle is largely irrelevant, and science does a much better job of predicting and explaining our experiences.
Weak Measurement
The notion of 'weak measurement' is reasonable simple, and was first proposed 30 years ago [2]. The reason for the Uncertainty Principle is often understood in terms of the 'collapse of the wavefunction'. A photon or electron propagates in a wave-like manner, but when we take a measurement we collapse the wavefunction and require the thing we measure to take on a specific value. When we collapse the wavefunction for velocity, we increase the uncertainty for position, and vice versa. The idea of taking a 'weak measurement' is to take a quite imprecise measurement of a quantity. By (metaphorically) sneaking a peek from the corner of our eye, we take less information from the wavefunction, causing it to collapse to a lesser extent. This allows it to retain more precision in the other of the paired quantities - momentum or position.
Two teams of experimental physicists, apparently working independently, both published papers on weak measurements in 2011. Interestingly, one team conducted weak measurements of momentum coupled with strong measurements of position, while the other did the reverse, demonstrating that both options are possible.
A team led by Jeff Lundeen at the Canadian Institute for National Measurement Standards [3] weakly measured the position of photons multiple times and averaged these weak measurements together to gain more information. They then strongly measured the momentum of the same photons (introduced to the apparatus one at a time) using 'post-selection'. That is, they used only the position measurements of the photons that, when measured later, turned out to have a particular momentum. Their paper is very interesting, since they claim that these measurements actually allow them to measure the wavefunction itself. This is fascinating, since some interpretations of quantum mechanics consider that the wavefunction is only a metaphor or a mathematical formalism that allows calculations to be made, not a physical, measurable property of the universe.
An international team led by Sacha Kocsis conducted the reverse experiment (actually, the differences between the two experiments are far greater than that, I am oversimplifying, but the papers are in the references below if you want far more detail), conducting weak measurements on the momentum of photons and then strong measurements through post-selection for their position.
Conclusion
It's an intriguing set of experiments and possibilities. Very smart quantum physicists I've spoken with think that there's no additional information gained by this method, but it will be interesting to watch developments in the work of the Lundeen and Koscis teams and other scientists working in this space. After all, it was Einstein prying at the cracks and loose ends of 19th century physics like the photoelectric effect that got us to quantum in the first place (with contributions from many others, of course). Who knows where sneaking around while 'Heisenberg is not looking' might get us?
References
[1] Heisenberg, W. (1927) “Ueber den anschaulichen Inhalt der quantentheoretischen Kinematik and Mechanik” Zeitschrift für Physik 43, 172-198. English translation in Wheeler, J.A. and Zurek, W.H. (eds) (1983) Quantum Theory and Measurement (Princeton NJ: Princeton University Press), pp. 62-84.
[2] Aharonov, Y., Albert, D.Z. & Vaidman, L. (1988). How the result of the measurement of a component of the spin of a spin-½ particle can turn out to be 100. PhysRevLett, 60, 1351-1354. DOI:10.1103/PhysRevLett.60.1351
[3] Lundeen, J.S., Sutherland, B., Patel, A., Stewart, C. & Bamber, C. (2011). Direct measurement of the quantum wavefunction. Nature, 474(7350), 188-191. DOI:10.1038/nature10120.
[4] Kocsis, S., Braverman, B., Ravets, S., Stevens, M.J., Mirin, R.P., Shalm, L.K. & Steinberg, A.M. (2011). Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer. Science, 332(6034): 1170-1173. DOI:10.1126/science.1202218
Notes
A slightly more formal version I wrote of some of these same ideas is available at: https://arxiv.org/abs/1306.2991
A quick side note: this post has nothing to do with Walter White or Breaking Bad, despite the fact that 'Heisenberg' was a code name used by that character in that show.
And another: I published an academic paper in education research using a similar title. I have written this article from scratch but like the title... and it's only self-plagiarism.