The Michelson-Morley Experiment

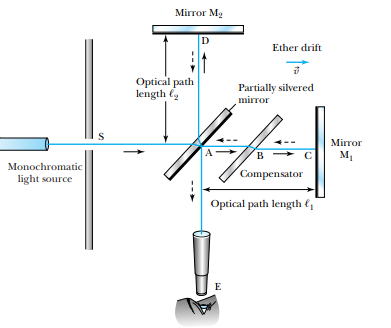
The Earth orbits around the sun at a high orbital speed, about 10 4 c, so an obvious experiment is to try to find the effects of the Earth’s motion through the ether. Even though we don’t know how fast the sun might be moving through the ether, the Earth’s orbital velocity changes signifi cantly throughout the year because of its change in direction, even if its orbital speed is nearly constant. Albert Michelson (1852– 1931) performed perhaps the most significant American physics experiment of the 1800s. Michelson, who was the first U.S. citizen to receive the Nobel Prize in Physics (1907), was an ingenious scientist who built an extremely precise device called an interferometer, which measures the phase difference between two light waves. Michelson used his interferometer to detect the difference in the speed of light passing through the ether in different directions. The basic technique is shown in Figure 2.2. Initially, it is assumed that one of the interferometer arms (AC) is parallel to the motion of the Earth through the ether. Light leaves the source S and passes through the glass plate at A. Because the back of A is partially silvered, part of the light is reflected,eventually going to the mirror at D, and part of the light travels through A on to the mirror at C. The light is reflected at the mirrors C and D and comes back to the partially silvered mirror A, where part of the light from each path passes on to the telescope and eye at E. The compensator is added at B to make sure both light paths pass through equal thicknesses of glass. Interference fringes can be found by using a bright light source such as sodium, with the light fi ltered to make it monochromatic, and the apparatus is adjusted for maximum intensity of the light at E. We will show that the fringe pattern should shift if the apparatus is rotated through 90° such that arm AD becomes parallel to the motion of the Earth through the ether and arm AC is perpendicular to the motion. We let the optical path lengths of AC and AD be denoted by /1 and /2, respectively. The observed interference pattern consists of alternating bright and dark bands, corresponding to constructive and destructive interference, respectively (Figure 2.3). For constructive interference, the difference between the two path lengths (to and from the mirrors) is given by some number of wavelengths, 21/1 /2 2 nl, where l is the wavelength of the light and n is an integer. The expected shift in the interference pattern can be calculated by determining the time difference between the two paths. When the light travels from A to C, the velocity of light according to the Galilean transformation is c v, because the ether carries the light along with it. On the return journey from C to A the velocity is c v, because the light travels opposite to the path of the ether. The total time for the round-trip journey to mirror M1 is t1: t1 /1 c v /1 c v 2c/1 c 2 v 2 2/1 c a 1 1 v 2/c 2 b Now imagine what happens to the light that is reflected from mirror M2. If the light is pointed directly at point D, the ether will carry the light with it, and the light misses the mirror, much as the wind can affect the flight of an arrow. If a swimmer (who can swim with speed v2 in still water) wants to swim across a swiftly moving river (speed v1), the swimmer must start heading upriver, so that when the current carries her downstream, she will move directly across the river. Careful reasoning shows that the swimmer’s velocity is 2v 2 2 v 1 2 throughout her journey (Problem 4). Thus the time t2 for the light to pass to mirror M2 at D and back is t2 2/2 2c 2 v 2 2/2 c 1 21 v 2/c 2 The time difference between the two journeys t is ¢t t 2 t1 2 c a /2 21 v 2/c 2 /1 1 v 2/c 2 b (2.3) We now rotate the apparatus by 90° so that the ether passes along the length /2 toward the mirror M2. We denote the new quantities by primes and carry out an analysis similar to that just done. The time difference t œ is now ¢t œ t 2 œ t 1 œ 2 c a /2 1 v 2/c 2 /1 21 v 2/c 2 b (2.4) Michelson looked for a shift in the interference pattern when his apparatus was rotated by 90°. The time difference is ¢t œ ¢t 2 c a /1 /2 1 v 2/c 2 /1 /2 21 v 2/c 2 b Because we know c W v, we can use the binomial expansion* to expand the terms involving v 2/c 2, keeping only the lowest terms. ¢t œ ¢t 2 c 1/1 /2 2 c a 1 v 2 c 2 p b a 1 v 2 2c 2 p b d v 2 1/1 /2 2 c 3