C.D.Lin 的存在性定理有假

数学概念与其存在性定理是对应的，一定是先准确地定义概念，然后研究其存在性与解的是否唯一性。作者反复变换 LHD 概念去适应存在性定理，恰恰证明他们是先有存在性定理，这个定理一定不是自己导出来的。因为作者的LHD 定义域与文献的 LHD 不同构，它的存在性不意味着文献定义的 OLHD 的存在性。这就决定了他们不能证明该定理。

5.1 二者存在性定理的直接比较

5.1.1 He 的存在性定理及其证明

5.1.2 Lin 的存在性定理及其证明

定理的必要性部分与 He 的完全相同，关键参数 4k+2 所用字符奇妙地一致。其证明导言所描述的证明步骤仿佛就是从 He(2009) 的证明中抽出来的。

5.2 运行数2 的 OLHD 不存在是假命题

运行数 n 不能是 3，在零相关设计的情况下是正确的， He(2009) 给出了证明，置换集合 “S 中只有 6 个向量，任何两个的相关系数不为零。” 在 Lin(1008) 中，作者用 "it is easy to verify" 逃避命题的证明。在 Lin(2010) 中，作者说“Trivially, run size n cannot be two or three.” 这些说法都是不妥当的。事实上，在 Rao 定义下，OA_II(3,3,3,2) 存在 (Hedayat et al.(1999)p.133)。

当n=2 和 b 是实数时，((b,0)^T,(0,b)^T) 满足Taguchi 或 Hedayat 等的正交定义；内积为 0，满足代数学正交定义, 但非零相关。在Lin 定理中 4k+2 中的 k 不能是 0。

5.2 Lin 的存在性定理的必要性部分证明中逻辑严重失范

这个命题需要证明的是当 n=4k+2 (k=0,1,...)时置换集合中任何两个成员都不正交。Lin 没有回答这个问题。她的证明逻辑上严重失范。

作者指定 “a and b be first and second columns”. 而且 “Without loss of generality, we assume that a=......” 去推出矛盾，就做出结论，说任何两个置换都不正交。这个被指定的 a 是一个经过精心排列的特殊结构，不是一般。当一个向量不是此一结构时如何推理，Lin 没有说。Without loss of generality 使用不当。即使证明了这两个列不正交，并不能得出该置换集中任何两个向量不正交的结论。这顶多只证明了a 与它的其他置换不正交，而没有证明其他置换相互之间不正交。以 n=6 为例, 置换集合中共有 6!=720 个置换, 即使证明了a=(-1,-3,-5,1,3,5)^T 与其他 719 个置换都不正交，不能自然地得出 a 的其余 719 个置换的 258,121 种向量组合都不正交的结论。指定a 为一特殊形式，推出了矛盾就说结论成立，这个归纳不完全。用某集合中一个特殊成员推出了矛盾，用同一集合其他成员能不能推出同样的矛盾？这正是需要证明的，作者没有证明。利用特例证明命题逻辑之后，必须证明对集合中任何成员都能得到同样的结果。这才是完全归纳。作者没有完成这一步。正如我们不能“不失一般”指定一个整数去证明 1 至 n 的 n 个自然数的平方和计算公式成立，必须证明对任何正整数 n 公式都成立。数学课程中使用数学归纳法（完全归纳法）。如果能够像 Lin 博士这样使用“不失一般”，当然，你也可以轻而易举地证明哥德巴赫猜想和三等分角问题。

5.3 Lin 的证明中关键逻辑前提是假的

Lin 证明最重要的逻辑前提是 "both 2b_i and 2b_{i+n/2 are odd, i=1,...,n/2." 这只对水平间距离为奇数时有效，而对水平间距不为奇数时无效，推理不能继续，Lin 要的矛盾不能得到。这是 Lin 用 LHD2 定义 LHD 的奥秘。她没有说明如何处理水平间距不是 1 的情况，因此，她没有完成命题的证明过程。因为 LHD 概念被作者偷换，无法完成该证明。

作者的证明的必要性部分没有正确完成，至少还缺少三个步骤，现有的证明是不合逻辑的。这也恰恰证明了该命题不属于该作者。

5.4 存在性定理的充分性没有得到有效证明

正交超立方设计的构造是一类 NP Hard 难题，正交设计究竟有多少列是未知的，所以我们不能一般化地讨论其存在性问题。

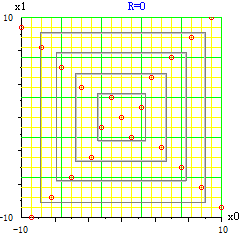
1. 在 Lin 的证明中顶多证明了 n≠4k+2 时可以构造出两正交列. 而不可能做到任给一个正整数 p, (n≠4k+2), 构造出所要求的结果。是否存在多于两列的 OLHD 的问题，该证明没有回答。

2. 用 Lin(2008)中的表 2.3 中的运行数为 6 的那个阵列与 O₂ 堆叠 29 次，那时 n=122，ρ²<<10^-10, 你定义它是什么？继续堆叠 300 次或1000次呢？

3. 一个试验设计 D 是一个区别于一般正交矩阵的正交设计，它不仅列正交，边际分布是均匀的，联合分布也应该是均衡的。Lin 的证明中构造的 OLHD 非常不均衡。

4. 运行数为 5 的OLHD 与 O₂ 堆叠四次的结果示于下图，

继续堆叠的结果是四条射线将无限延长，几乎就是×-形分布。

试验设计不应该接受这类分布的设计。某些二次曲面(例如抛物面和鞍形曲面)的准线是交叉的两条直线。假如过程的真实规律是抛物面或鞍形曲面，在两条交叉的直线上采样，必然把曲面判定为平面。这样的试验找不到优化区域，不能形成优化方案，整个试验失败，给出错误的结论。在工业试验中, 过程机理不明，经常用二次函数构造回归模型拟合实验数据，建立预报模型，寻找优化的方案，一定会遇到这种问题。完全线性过程很少见，用 X-形试验点分布，失败是大概率事件。

某些方法可以改善其均匀性，但不能保证对任何运行数存在。参见我的博客《同 C.D.Lin 等四博士讨论堆叠法构造正交超立方设计》

作者的命题没有得到有效证明。