WarArm team (The video game team I’m part of) is currently trying to improve the weapon’s gun experience that must be ergonomic for the player and must reflect a soldier who in war tries to aim right on target. We noticed over time that the soldier’s fire was too random in the scope of the target and the propagation of the projectiles took place in an uncontrolled manner. How to fix the problem? How to control the randomness of the bullets? Someone would just say to increase the accuracy and thus reduce the range of randomness, but so it becomes too easy for the player. We want more control of the weapon, it needs to shoot more in the center and less on the sides.
Let me explain with pictures

These 20 bullets were fired with a uniform casuality

This is what we want, 20 bullets that tend to be fired more towards the center
How to fix this problem?
My approach is to use the theory of probability and I therefore decided to help me with the wonderful gaussian function. Gaussian function appears as the density function of the normal distribution and we will use this.
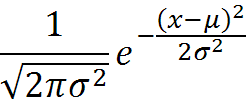
We must consider this function with μ = 0 and σ = “weapon accuracy“. This values transform our “normal distribution” into a “normal standard distribution” density function. We have a density that has the following graph and has mean values at zero point. Zero point will be the center of our screen, where the shots should go. If at point x, the corresponding f(x) is high then there is more chance that the shot goes to that point.
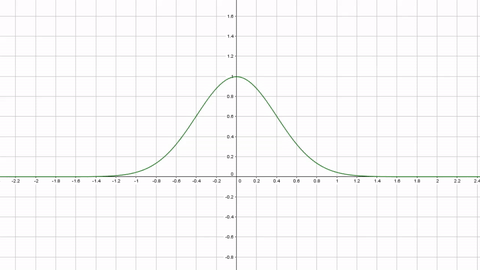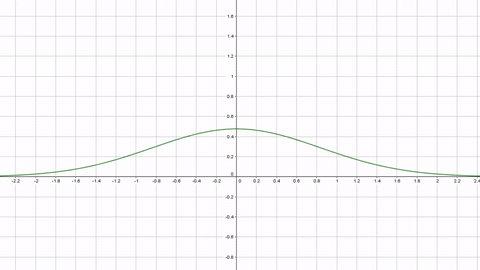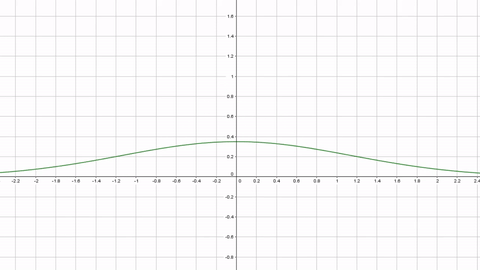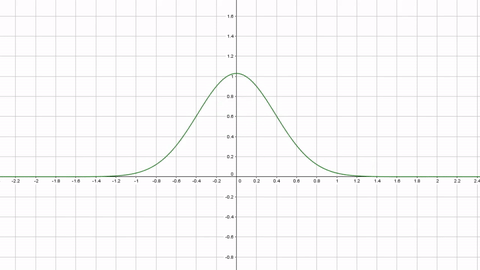
By varying the “weapon accuracy” (zero is the center of the screen)
It all seems complicated but …
This formula does not seem easy to apply. The computer fails to generate randomness of this type, because the random features available in the basic libraries of most languages are of uniform distribution. That is, uniform randomness over a range [a, b) such as the bullets distribution in the first image. Searching and searching I found a way that allows us to approximate normal distribution starting from two randomly uniformly distributed variables (which we have available with any function that generates a random number).
Box–Muller transform
Here we are finally at the heart of the matter. Now we understand how to generate random numbers so as to simulate the will of the soldier to shoot tensely toward the center rather than at random in a spherical range. To get to a normal distribution we use the Box–Muller transform for generating standard, independent, normally distributed with zero expectation, unit variance (that we will change) random numbers, given a source of uniformly distributed random numbers.
This transformation get in input two-dimensional continuous uniform distribution to give in output a normal distribution. If x1 and x2 are our two random generated values between 0 and 1, we can use these random variables in this formula to get a normal distributed value:
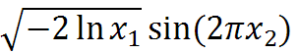
At the same formula can be applied the cosine
Code example in C#
double RandomNormalDistribution(double mean = 0, double stdDev = 1f) //mean = 0 is the center of the screen
{
//uniform in (0,1] interval
double x1 = (1.0 - rand.NextDouble());
double x2 = (1.0 - rand.NextDouble());
double randStdNormal = mean + stdDev * (Math.Sqrt(-2.0f * Math.Log(x1)) * Math.Sin(2.0f * Math.PI * x2)); //normal(mean, stdDev)
return randStdNormal;
}
This is an example of use:
//You can change the accuracy value (remember to leave the mean to zero, is the center of the screen)
double ErrorX = RandomNormalDistribution(stdDev: Accuracy);
double ErrorY = RandomNormalDistribution(stdDev: Accuracy);
The two error variables (ErrorX and ErrorY) will be used to define the point of the shot. Firing several shots you will notice that they will tend toward the center! It will no longer be a totally random shot. I wonder if the best games on the market will use a similar technique.
What do you think of this idea?
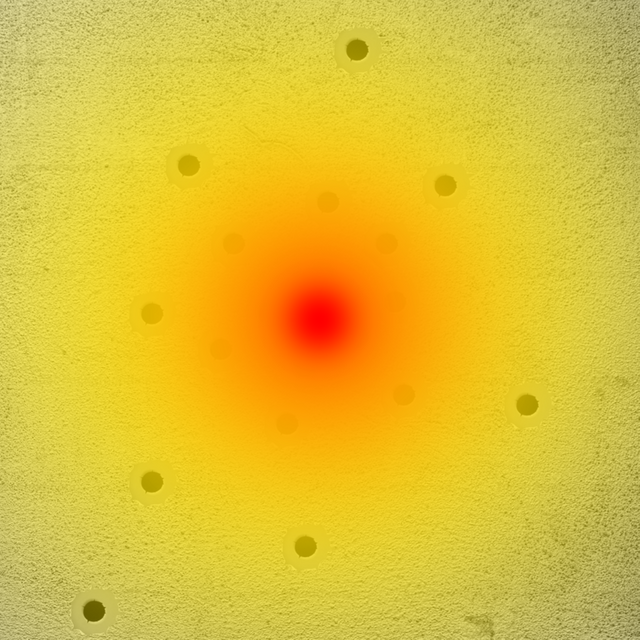
Firing probability: red very likely. Yellow unlikely
Polar form (computationally faster)
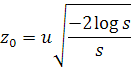
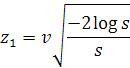
Do you want to know more about these two formulas? Visit my blog.

Ti chiedo un chiarimento di una cosa. Se ho ben capito per approssimare una distribuzione gaussiana utilizzi una formula che necessita in imput di due numeri casuali tra 0 e 1. Quei numeri casuali come vengono generati? La logica che usa il computer per stabilire quale numero far uscire casualmente può incidere significativamente su quanto è corretta l'approssimazione che stai cercando di ottenere? Ci sono funzioni che generano numeri causali "più casualmente" di altre o comunque siano più utili al tuo scopo?
Bel post comunque, solo per la gaussiana meriteresti un centinaio di voti :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ciao, le funzioni standard dei vari linguaggi generano numeri pseudocasuali con probabilità uniforme, queste sono testate affondo da chi le ha create attraverso dimostrazioni matematiche che verificano sia effettivamente così. Il teorema di Box-Muller è infatti molto potente perché presi in ingresso due numeri casuali con probabilità uniforme permette di avere altri due numeri con probabilità su gaussiana! Quindi, dato che un computer non può generare numeri su gaussiana, ma solo numeri con probabilità uniforme, questa permette di avere valori normali attraverso quelle formule matematiche.
"Ci sono funzioni che generano numeri causali "più casualmente" di altre o comunque siano più utili al tuo scopo?" Ci possono essere funzioni più efficaci, che generano un grande intervallo di valori casuali, ma ricordiamo sempre che i valori sono pseudo casuali, cioè prevedibili, generati da un seed di input.
Grazie!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sono una frana a matematica... ma super-interessante quello che fai.
Finché rimane virtuale, tutto ok ;-)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Il mondo virtuale esiste per sperimentare le proibizioni del mondo reale che vanno dai limiti del nostro corpo ai limiti fisici, a dimensioni spaziali diverse e tutto quel che si può immaginare, infatti è come giocare con ciò che ha immaginato chi ha programmato il gioco. Entriamo nella finzione per conoscere quello che non potremo mai fare e non è meraviglioso tutto questo? E' un modo per allargare gli orizzonti creativi, per porsi nuove domande.
Ovviamente quello che posso dire è che non bisogna esagerare al tal punto di finire per confondere la realtà con la finzione, reputando la finzione più vera della realtà stessa.
Grazie del commento, e ricorda che la matematica è la regina delle scienze, utile ovunque e dà senso ad ogni cosa, una volta compresa ovviamente :D !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grazie mille per la risposta dettagliata ;-)
Io personalmente mi baso su principi buddisti... causa-ed-effetto... azione-reazione.
Son messo male con la matematica.
P.S. è da un po' che non gioco ai videogames... Utilizzavo il Commodore64 fino alla Play2... poi qualche app game in android.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Non ho ben capito l'ultima sillaba del tutto.Ahaahhaha, complimenti !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You rock 😊
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Tutto chiarissimo .-.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Nun je la posso fa'.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit