The Sieve of Eratosthenes is an algorithm for finding prime numbers in a range. Conceptually, it's a very simple algorithm. Let's assume our range is always [2, n]. In our examples, we'll consider n=100.
In order to follow along, you will need knowledge of basic math and Python programming.
Intuition
Consider a list of all the numbers in this range:
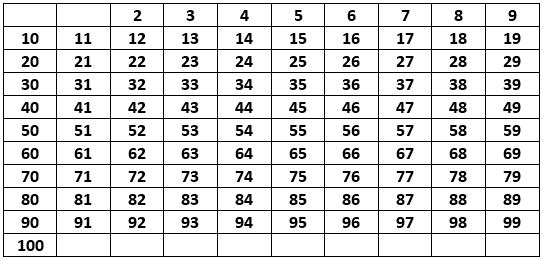
At each step, the first unmarked number in this list will be prime, so we can add it to our list of prime numbers. We will mark these with a green background.
After this, we will eliminate all the multiples of the most recently discovered prime number from our list. Since they are multiples of a prime number, they are obviously not prime. We will mark these with an orange background.
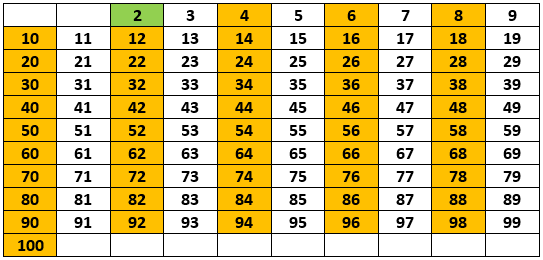
So far this works: 2 is the first prime, 3 is the next one, then 5 and so on. Our list will look like this in the end:
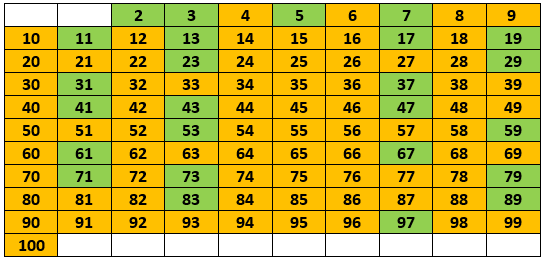
So why does this work? Consider the standard primality test algorithm: for each number up until the square root of the number x you're checking, you verify if x is divisible by that number: if yes, it's not prime. If you didn't find any it's divisible by, then it's prime.
What would happen if you used that algorithm to generate prime numbers? It would check the same things multiple times: the integer parts of the square roots of 89 and 97 are the same, but you will iterate all those numbers twice, when once would've been enough to tell you that both 89 and 97 are prime.
The sieve manages to avoid this repetition by using the eliminate-all-multiples trick described above.
This will lead to an O(n log log n) (yes, that is log of log of n) time complexity and an O(n) memory complexity. There is a time vs memory trade-off here: we use more memory compared to using the primality test algorithm, but we get a better time complexity. We'll see later how this translates to practical performance.
Naive / reference sieve implementation
The following is a naive implementation of the method described above: we create a list of length n+1, initially with zeros. We will use the following notation in code:
sieve[i] = 0means that i is prime (initially we assume that all numbers are prime)sieve[i] = 1means that is definitely not prime.
The code:
def sieve_naive(n):
sieve = [0] * (n+1)
for i in range(2, n+1):
if sieve[i] == 0:
# i is prime, eliminate its multiples
for j in range(i+i, n+1, i):
sieve[j] = 1
return [p for p in range(2, n+1) if sieve[p] == 0]Let's also write a basic primality check method and time the two:
def with_primality_check(n):
def is_prime(n):
if n < 2:
return False
if n < 2:
return True
if n % 2 == 0:
return False
d = 3
while d*d <= n:
if n % d == 0:
return False
d += 2
return True
return [p for p in range(2, n+1) if is_prime(p)]Note that the above code also enjoys some optimizations. We have not yet optimized the sieve at all.
Consider this basic test code:
from time import time
n = 1000000
t_start = time()
sieve = sieve_naive(n)
t_end = time()
print('Time for the naive sieve for n = {}: {}s'.format(n, t_end - t_start))
t_start = time()
primality_checker = with_primality_check(n)
t_end = time()
print('Time for the primality check method for n = {}: {}s'.format(n, t_end - t_start))
# to make sure we don't have a mistake somewhere
assert sieve == primality_checkerOn my machine, this prints:
Time for the naive sieve for n = 1000000: 0.4687223434448242s Time for the primality check method for n = 1000000: 7.813140869140625s
A considerable improvement already. But let's do better! In the following, the same test code will be used. We will only show the output.
Basic optimizations
Let's start by adding the optimizations that our primality check method above has:
- Eliminate multiples of
2separately, start from3and move in increments of2 - Only iterate until the square root of
n.
The changes are quite trivial:
def sieve_v2(n):
sieve = [0] * (n+1)
# sqrt(x) == x to the power of (1/2)=0.5
for i in range(3, int((n+1) ** 0.5), 2):
if sieve[i] == 0:
# i is prime, eliminate its multiples
# this time, we can start from its square.
# The rest have been eliminated by smaller
# values of i.
for j in range(i*i, n+1, i):
sieve[j] = 1
return [2] + [p for p in range(3, n+1, 2) if sieve[p] == 0]Some results:
Time for the naive sieve for n = 5000000: 2.342332363128662s Time for sieve v2 for n = 5000000: 0.9467916488647461s
A more than 2x improvement!
Memory improvements
First of all, notice that we completely ignore even positions in our sieve list. Therefore, a list half the size of n would suffice. This is currently left as an exercise. I will present the solution in Part 2. Note that it's not as trivial as it may sound, mainly because of our square root optimization.
Another improvement is using only a single bit for each element in our list. This doesn't apply to Python however: Python will use as many bits as the values require, so in our case, it will use a single bit for each list element by default and we don't have to do anything. In other programming languages however, you might declare sieve as an array of 32 bit integers. That would mean 32 times more memory than necessary!
The following code shows how you can use bitwise operators to optimize the memory usage (and also the execution time) in such languages. We use the get and set functions for accessing and setting the necessary bits in our list, taking into account that each element has 32 bits.
Note: like I said above, Python already does this for you. If you run the code below in Python, it will actually be slower, because you're just adding overhead. This is only to see how it would be done in other programming languages.
def sieve_v3(n):
# 32 = 2**5
def get(array, position):
return (array[position >> 5] >> (position & 31)) & 1
def set(array, position):
array[position >> 5] |= 1 << (position & 31)
# same as before, just use
# the helper functions for accessing the sieve
sieve = [0] * (n//32+1)
for i in range(3, int((n+1) ** 0.5), 2):
if get(sieve, i) == 0:
for j in range(i*i, n+1, i):
set(sieve, j)
return [2] + [p for p in range(3, n+1, 2) if get(sieve, p) == 0]Recall that, considering integers and integer results:
x << kis equivalent to multiplyingx<<by2to the power ofk;x >> kis equivalent to dividingxby2to the powerk;x & (2**k - 1)is equivalent tox % (2**k);x |= 1 << ksets thekth bit ofx(from right to left, counting from 0).
I suggest you run a few examples on paper to really understand what is going on with the bitwise operations.
In part 2 I will cover the following. Feel free to try to figure these out on your own before reading my take on them.
- How to not allocate memory for even numbers;
- How to implement a sieve for any range [x, y];
- How to implement a wheel.
Hey @ivlad, great post! I enjoyed your content. Keep up the good work! It's always nice to see good content here on Steemit! Cheers :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @ivlad! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit