Solution
The problem of this contest was to find the first zero on the critical line of the riemann zeta function using the following formula:
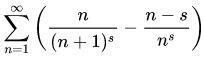
I implemented an example solution in java (using a self written implementation of complex numbers which isn't explicitely linked here):
public class ZeroFinder {
public static Complex zeta(Complex in, int n) {
Complex res = new Complex(0, 0);
for(int j = 1; j < n; j++) {
res = res.plus(in.negate().times(Math.log(j+1)).ePow().times(j).minus(in.negate().times(Math.log(j)).ePow().times(in.negate().plus(j))));
}
return res;
}
public static void main(String [] args) {
// Find the first 10 zeros in the real part:
int [] list = new int[10];
int index = 0;
Complex last = new Complex(0, 0);
for(int i = 1; index < 10; i++) {
Complex next = zeta(new Complex(0.5, i/10.0), 1000);
//System.out.println(next);
if(last.r*next.r < 0) { // Check if the value of r changes sign
list[index] = i;
index++;
}
last = next;
}
// Look at the first zeros in more detail and check if there is also an imaginary zero:
double y0 = 0;
outer:
for(int i = 0; i < 10; i++) {
last = new Complex(0, 0);
for(int j = 0; j < 1000; j++) {
double y = list[i]/10.0+j/1000.0-0.5;
Complex next = zeta(new Complex(0.5, y), 10000);
if(next.i*last.i < 0) { // Check if the value of i changes sign
y0 = y;
break outer;
}
last = next;
}
}
// Look at the region in even more detail:
double resI = 0, resR = 0;
last = new Complex(0, 0);
for(int i = 0; i < 1000; i++) {
double y = y0+(i-500)/10000.0;
Complex next = zeta(new Complex(0.5, y), 1000000);
if(next.i*last.i < 0) { // Check if the value of i changes sign
resI = y;
}
if(next.r*last.r < 0) { // Check if the value of r changes sign
resR = y;
}
last = next;
}
System.out.println((resR+resI)/2); // Print the average of resR and resI which should be more accurate.
}
}
This code prints the result 14.1332 which is not perfectly accurate even though I used 1000000 iterations in the final run.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | Solution found | |
|---|---|---|
| @tonimontana | 14.141171601414683 | A lot of digits for the fact that the fourth digit is already off. |
| @crokkon | 14.1 |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winners:
As promised 2 SBI for everyone!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Do we even know that the zeros of the truncated sum have anything to do with the zeros of the real function? Like say you have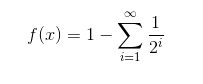 Then f is 0 but all the finite sums have no zeros.
Then f is 0 but all the finite sums have no zeros.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
There is an important difference between the sum I chose and the function you show:
Your function won't give a graph where you could read the zeros( by checking for sign changes).
If you have a sum that converges then you can conclude that your graph will be within some small range ε of the graph of the infinite sum. So the zeros you can read in the partial sum graph should also closely match those in the infinite sum graph.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit