
Hoje é 29/fev/2020. Logo, 2020 é ano bissexto.
2020 é ano bissexto. E por isso temos um dia a mais, exatamente o dia de hoje, 29/fevereiro.
Onde fica "escondido" este dia extra que reaparece a cada quatro anos?
A ideia não é complicada. Um ano solar¹, também chamado de ano trópico, sem maiores complicações, é o tempo que o nosso planeta demora para completar uma volta ao redor do Sol. E, embora o ano nos calendários tenha exatos 365 dias inteiros, na prática este valor é ligeiramente maior e tem casas decimais.
Correção aproximada
Quando você quer dar uma explicação rápida para ano bissexto, sem entrar em detalhes, basta dizer que 1 ano solar = 365,25 dias. Logo, a Terra dá uma volta no Sol a cada 365,25 dias. Na prática, a cada volta completa da Terra ao redor do Sol, há uma "sobra" de 0,25 dia, ou seja, 1/4 de dia.
![ano_bissexto_Juliano_fra[1].jpg](https://steemitimages.com/640x0/https://cdn.steemitimages.com/DQmWnK4AaYZo4gSR8Y4Tze96BsMjLxNo9My1pmrSihPoPHL/ano_bissexto_Juliano_fra[1].jpg)
Note que 1/4 de dia, "diluído" ao longo de um ano, passa despercebido. Mas o efeito cumulativo, ao longo de vários anos, é terrível! Se não é feita uma correção, as datas de início as estações do ano (no calendário) ficam defasadas das estações do ano reais ligadas às sucessivas posições da Terra ao redor do Sol.
Tendo em vista o valor 1 ano solar = 365,25 dias, conhecido e considerado pelo Calendário Juliano de antes de Cristo, com uma "sobra" de 1/4 de dia a cada volta da Terra ao redor do Sol, basta ir juntando as "sobras" e, a cada quatro anos, a "sobra" total acumulada corresponderá exatamente a 1 dia pois 4 x 0,25 = 1 dia.
A correção, neste caso, é óbvia: a cada quatro anos acrescentamos 1 dia ao calendário anual. E "encaixamos" este dia onde quisermos, hipoteticamente zerando a "sobra".
![ano_bissexto_Juliano_cor[1].jpg](https://steemitimages.com/640x0/https://cdn.steemitimages.com/DQmd7Vav8hsABg2vxyBJdtHXZgBDpFcN5Kt8R6y8EuMZMYY/ano_bissexto_Juliano_cor[1].jpg)
Por razões históricas, este dia — que poderia ser "encaixado" em qualquer mês ao longo do ano — vem sempre ao final de fevereiro que, em vez dos tradicionais 28 dias, passa a ter 29. E temos um ano maior, com um dia extra, o ano bissexto.
A ideia da correção é mostrada na imagem abaixo, propositalmente fora de escala, e que aproxima a órbita da Terra ao redor do Sol para uma circunferência.
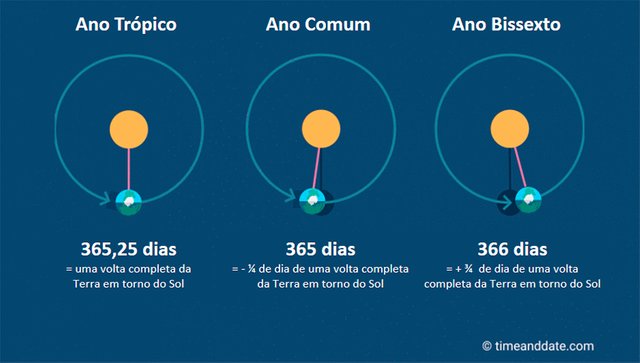
Ano solar (ou trópico) X ano comum X ano bissexto. (adaptado de timeanddate.com)
Mas há um "probleminha" nesta correção...
Sim, tem um "probleminha", assim mesmo no diminutivo, nesta tentativa de "encaixar" no calendário 1 dia exato a quatro anos.
1 ano solar, uma volta da Terra ao redor do Sol, não corresponde exatamente a 365,25 dias. A melhor medida que temos é de 1 ano = 365,242199 dias.
![ano_bissexto_Moderno_dec[1].jpg](https://steemitimages.com/640x0/https://cdn.steemitimages.com/DQmYDoYmM3Jp7Z79ReAwjEh2K4tfzp2vgXv93EgDMQg4kUx/ano_bissexto_Moderno_dec[1].jpg)
E 4 x 0,242199 = 0,968796, ou seja, não dá exatamente 1 dia (valor redondo)!
A diferença é minúscula: 1 - 0,968796 = 0,031204. Pouco mais de três centésimos. Por isso chamei de "probleminha". Mas é um erro que, ainda que muito pequeno, não é desprezível quando pensamos no acumulado ano após ano. Este erro também precisa ser corrigido.
Muito louco isso, não? Ao tentarmos corrigir a "sobra" de quase 1/4 de ano a cada quatro anos, colocamos 0,031204 de dia mais! Tetando acertar, ainda erramos!
A ideia do ano bissexto, como eu disse acima e aqui repito, não é complicada. Basta entender que o ano solar não é um número inteiro de dias.
A correção para o ano solar "quebrado", no entanto, não é nada trivial. Dá para perceber a "encrenca"?
A melhor correção possível
Com a ajuda da Matemática, podemos verificar que a "sobra" de 0,242199 dia equivale a uma sequência de somas e subtrações de frações. Veja:
![ano_bissexto_Moderno_cor[1].jpg](https://steemitimages.com/640x0/https://cdn.steemitimages.com/DQmWbhgM1fV9HCyHjCd2g11t6XojcrGKJWafzaYTwbCzVra/ano_bissexto_Moderno_cor[1].jpg)
A melhor correção para definir se um ano é bissexto, ou seja, se vai ter 365 ou 366 dias, é:
A cada quatro anos somamos 1 dia ao calendário;
A cada 100 anos subtraímos 1 dia ao calendário;
A cada 400 anos somamos 1 dia ao calendário;
A cada 3300 anos subtraímos 1 dia ao calendário.
A quarta correção acima nunca foi feita porque ainda não se passaram 3300 anos depois da reforma gregoriana que aconteceu 1582 e estabeleceu o calendário moderno. A "encrenca" ficou para o futuro, para quem viver no ano de 4882 (4882 = 1582 + 3300).
Gostou do tema? Neste post (no Física na veia! | UOL Tilt) do final de 2015, antecipando a chegada de 2016 que seria (e foi) bissexto, aprofundei um pouco mais o assunto. Nele até proponho um algoritmo para descobrir se um ano passado foi ou um ano futuro será bissexto.
Assim como no post anterior (daqui da versão Steemit do blog), dentre outros tantos já publicados aqui e no UOL, a Ciência sempre presente em nossas vidas. Às vezes tão disfarçada que passa despercebida. Mas sempre presente.
Abraço do prof. Dulcidio. E Física (e Astronomia) na veia!

Este texto também foi publicado no Física na Veia! | UOL Tilt neste link.
Parabéns, seu post foi selecionado pelo projeto Brazilian Power, cuja meta é incentivar a criação de mais conteúdo de qualidade, conectando a comunidade brasileira e melhorando as recompensas no Steemit. Obrigado!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Obg!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider using the steemstem.io app and/or including @steemstem in the list of beneficiaries of this post. This could yield a stronger support from SteemSTEM.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Tks!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit