Mais Física por trás do acidente com os garotos da Tailândia

Você tem ideia de quanto tempo dura um cilindro de ar comprimido destes que são usados em trajes de mergulho? Saberia como usar a Física para estimar este tempo?

O consumo de oxigênio, tanto pelos mergulhadores quanto pelos resgatados, deve ter sido um ponto bem crítico na operação de salvamento dos garotos da Tailândia. Concorda?

Se não faz a menor ideia, acompanhe o meu raciocínio.

Antes, um toque. Falei sobre a Física do resgate dos garotos da Tailândia no post anterior. Se ainda não leu, dá uma olhada lá.

Usando um modelo "furado"

Vamos imaginar um cilindro rígido de metal com 9 L de volume completamente cheio de ar comprimido a uma pressão de 200 atm. Um adulto em mergulho consome em média 40 L/min de ar. Vamos tratar esse valor como sendo um fluxo Φ de ar. Assim:

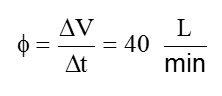
O tempo Δt de duração de um cilindro de ar com volume total ΔV = 9 L sendo consumido a uma taxa Φ = 40 L/min deve ser:

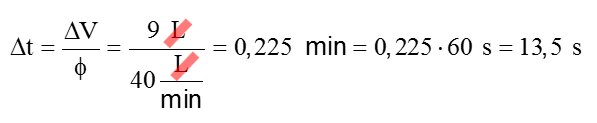
Opá! Tem algo errado aí! Um cilindro de mergulho não pode durar meros 13,5 s! Concorda?

Você consegue enxergar onde está o erro?

Usando um modelo mais adequado

No cilindro não temos apenas 9 L de ar. São 9 L de ar comprimido! Imagine que as moléculas do gás estão bem "socadas" lá dentro, forçadas a ficarem bem próximas, diminuindo os espaços vazios entre elas. Por isso mesmo a pressão interna no cilindro é altíssima, estimada em 200 atm, duzentas vezes maior do que a pressão normal do ar ao nível do mar. Assim, se pensar bem, vai concluir que tem muito ar dentro cilindro.

E tem outro detalhe crucial: se injetarmos ar a uma pressão de 200 atm na boca do mergulhador, certamente vamos explodir seus pulmões! Bem capaz até mesmo de estourar o crânio do cara! O ar não pode entrar no corpo de uma pessoa numa pressão assim tão alta! Concorda?

O segredo é usar um redutor de pressão. Com este dispositivo o ar sai do cilindro com pressão de 200 atm mas entra na boca do mergulhador a 1 atm, valor de pressão muito próximo ao que estamos acostumados a respirar. Dessa forma teremos as moléculas menos "apertadas", ocupando um volume significativamente maior. E, na prática, isso significa mais ar para respirarmos. E mais ar significa maior autonomia do cilindro debaixo d'água.

Por simplicidade, vamos supor que o ar comprimido possa ser tratado com um gás ideal¹. Assim podemos usar a Lei Geral dos Gases Ideais derivada da Equação de Estado também conhecida como Equação de Clapeyron². E teremos:

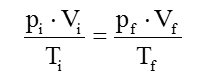
Os índices "i" e "f" significam "inicial" e "final", sendo a situação inicial àquela que corresponde ao gás dentro do cilindro e "final" ao gás fora do cilindro, pronto para ser respirado.

Supondo que o gás estará sempre na mesma temperatura, então T_i = T_f. A Lei Geral, para o caso de temperatura constante (transformação isotérmica) fica assim:

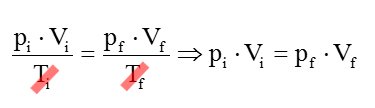
Substituindo os valores p_i = 200 atm, V_i = 9 L e p_f = 1 atm, podemos estimar o volume final V_f de ar respirável:

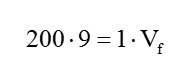
Resolvendo a expressão acima, encontramos o valor de V_f:

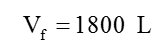
Note que 9 L de ar comprimido a 200 atm correspondem a 1800 L de ar respirável a 1 atm.

Conclusão: não há somente 9 L de ar para ser respirado e sim 1800 L!

1800 L de ar certamente propiciam uma duração bem maior do cilindro. De posse deste valor de volume de ar respirável podemos estimar o tempo Δt de duração (ou auonomia) do cilindro. Supondo que o fluxo de ar respirado seja Φ = 40 L/min e o volume total de ar disponível para respiração por nós calculado de ΔV = 1800 L teremos:

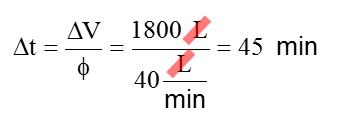
Agora sim! O cilindro, com as especificações consideradas, pode durar 45 min supondo taxa de consumo Φ = 40 L/min, valor bem razoável e bem próximo da autonomia real de um cilindro com esta suposta capacidade.

Um mergulhador experiente, que consiga controlar o fluxo respiratório, sem entrar em pânico, pode tentar baixar a taxa de respiração de Φ = 40 L/min para Φ = 30 L/min. Se conseguir, aumenta consideravelmente a autonomia do cilindro. Veja:

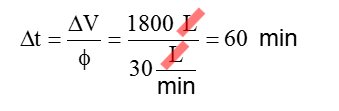
Respirando de forma mais calma e controlada, o mergulhador pode fazer o mesmo cilindro durar 60 min, ou seja, 1 h.

Percebeu a importância do controle da respiração para a autonomia durante um mergulho?

Foi por isso que resolveram sedar os resgatados no acidente da Tailândia, evitando pânico que poderia diminuir o tempo de uso dos cilindros de ar e até provocar afogamento. Veja detalhes no post anterior.

---

Mais uma vez reitero que a equipe de salvamento formada por mergulhadores tailandeses e outros mergulhadores estrangeiros foi muito inteligente e eficiente conseguindo controlar com muita segurança todos os fatores de risco da delicada operação de resgate. E por isso ela foi bem-sucedida!

Abraço do prof. Dulcidio. E Física na veia!

---

¹ Na prática, para que um gás se comporte como ideal, deve ser monoatômico, estar em alta temperatura e baixa pressão. O ar não é monoatômico. E no cilindro está em altíssima pressão. Aqui estamos fazendo uma simplificação apenas apara termos uma ideia do valor a ser estimado que, certamente, terá um erro. Mas, para teremos uma noção da ordem de grandeza do tempo de duração do cilindro, está valendo.

² A Equação de Clapeyron é p.V = n.R.T onde o trio (p,V,T), as variáveis de estado, são p (a pressão exercida pelo gás), V (o volume por ele ocupado) e T (a temperatura absoluta do gás). R é uma constante física. E n o número de mols.