In 1909 a scientist named Robert Millikan had made an experiment to find out the charge of an electron.
Before this, scientists had no way to measure the charge of an electron. Although they could find the mass to charge ratio with the mass spectrometer.
So, How did Robert Millikan do this? let's dive right in.
Firstly I should explain the outline of the experiment. But before that take a look at what the apparatus for this experiment would look like.
This is Millikan's oil drop apparatus.
And for its internal structure.
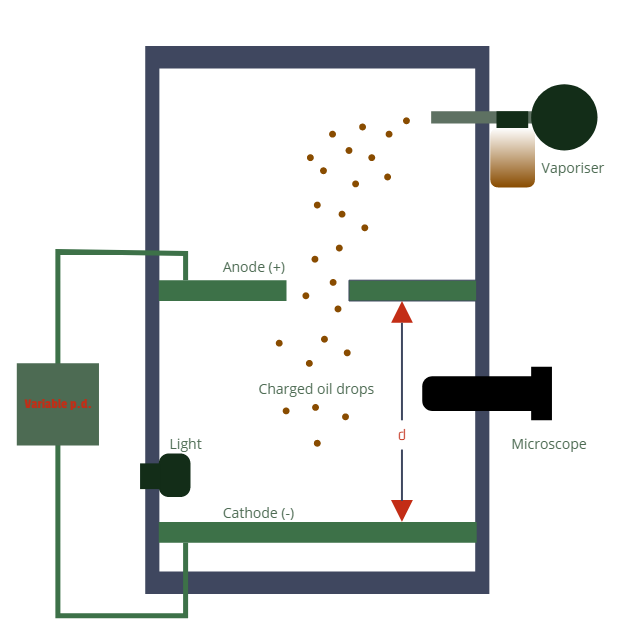
In this apparatus, Millikan performed various types of tests. like letting the oil drop fall at terminal velocity, balancing the weight of the oil drop with the electric field, providing a stronger force using the electric field then the oil drop's weight, stuff like that.
Okay, back to the beginning.
When the vaporiser is used, it sprays out oil droplet, which by friction gains electrostatic charge. also, keep in mind that the density of the air inside this apparatus is kept very low so that the pesky little upthrust won't bug us much. And this charge is always a multiple of the charge of an electron, as the drops either gain or lose some amount of electron. And due to gravity, the droplets continue it's way down, and some of them pass through the anode into the uniform electric field in between the charged plates ( anode and cathode). Or to find the terminal velocity (which is required later on) we just keep the switch off so there is no p.d. charging the plates.
You know what?
Let's just deal with the terminal velocity now!
But first, a little about stokes law.
Stoke's law is comprised of a equation derived from investigating fluid dynamics by Sir George Gabriel Stokes.
This equation was meant for low speed small sphere moving through a fluid.
F=6πηvr
In the equation
r -> radius of sphere
v -> velocity of sphere (this is where the terminal velocity comes in)
η -> coefficient of viscosity of fluid
So, back to Oil Drop
When the drop is under terminal velocity, that means all forces are balanced. Therefore
Weight = Viscous Drag
m g = 6 π η(viscosity of air) vₜ r(radius of sphere)
And then there is when the drop is held using electric force. That time the equation is,
weight=electric force
m g = E Q
but,
m g = VQ/d will be more viable here
Now, in both equation, we have weight in common
So, a new equation
VQ/d = 6πηvₜ r
Now we are getting somewhere
because
Q=(6πηvₜ rd)/V
But the only problem is, there is no way to measure the raduis for Millikan...
So the only thing he could do... Make equation bigger...
by substituting r from a further developed version of stokes law...
vₜ=(2r²g(ρₒᵢₗ-ρₐᵢᵣ))/9η => r=((9ηvₜ)/(2gρₒᵢₗ))^(½)
... Where did ρₐᵢᵣ go from the equation?...
uhh... Remember how Millikan kept the desity of air in the chamber very low, low enough to be negligible... Yeah, exactly that happened.
Now Millikan could finally find it... YAY
with,
Q= ((6πηvₜ d)/V)×((9ηvₜ)/(2gρₒᵢₗ))^(½)
In the end what Millikan found was,
Q= 1.59×10⁻¹⁹ C
which was infact only 1% away from the original value...
which was,
Q=1.602×10⁻¹⁹ C