How to draw an evolutionary tree II: maximum parsimony

In my previous post, I described how to use the algorithm UPGMA to construct an evolutionary tree from a distance matrix. It was fast and straightforward, but we had to make the assumption that evolution took place at the same rate throughout the tree. The next method, maximum parsimony, does not assume this and conceptually it is as simple as UPGMA. The drawback is that maximum parsimony is a lot slower. UPGMA singles out the optimal tree, under the assumptions of the algorithm, and does not attempt to score any other tree. Using maximum parsimony, you need to check all possible trees one at a time (there are probably algorithms that can speed up this process, but I don't know them).

Maximum parsimony assumes that the correct tree is the one that requires the fewest evolutionary changes. The rationale is this: Every evolutionary change is an event with a probability below 1. If you consider two such events, the probability that both of them happen is lower than the probability that just one of them does. Just like rolling two sixes with a pair of dice is less probable than rolling six with one of them.

To apply maximum parsimony, we first need a hypothesis about the relationship between the taxa we want to investigate. We will look at five taxa, labeled A-E, and postulate the following phylogeny:

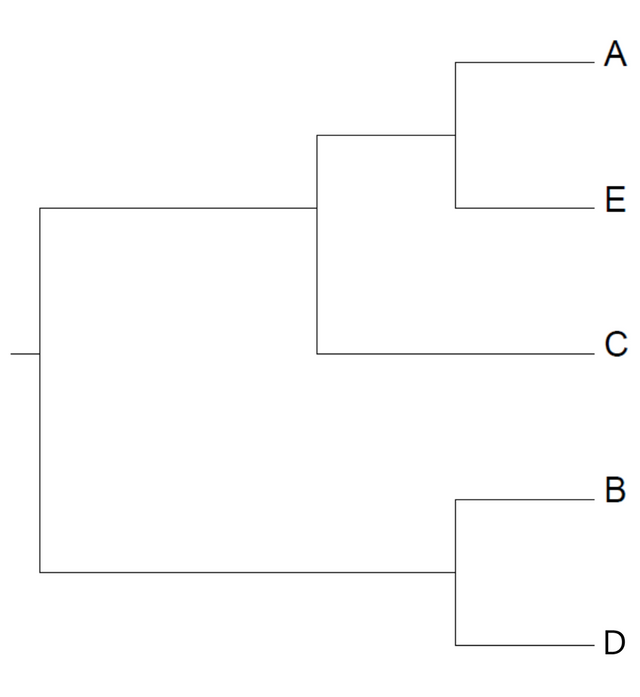
Now, our task is to check how probable this tree is. Or rather, how parsimonious. Unlike UPGMA, there is no need for a distance matrix. We just need to know a set of traits and how they appear in our taxa. Using molecular data, these traits would be bases in a DNA or RNA sequence, or amino acids in a protein. First, write up the set of traits in each taxon. Disregard any trait that does not differ between taxa, or differs in a single taxon only. Next, we could try to assume an ancestral state, i.e. the set of traits at the root of the tree. But this would be guessing, and guesses are usually time-consuming. Instead, we can apply a method known as Fitch's algorithm.

Instead of assuming anything about the root of the tree, we start from the leaves (the taxa) and work our way down, one trait at a time. Because this is just an example, we will only look at one trait here. Let's replace the names of the taxa with the trait, a DNA base from a particular locus:

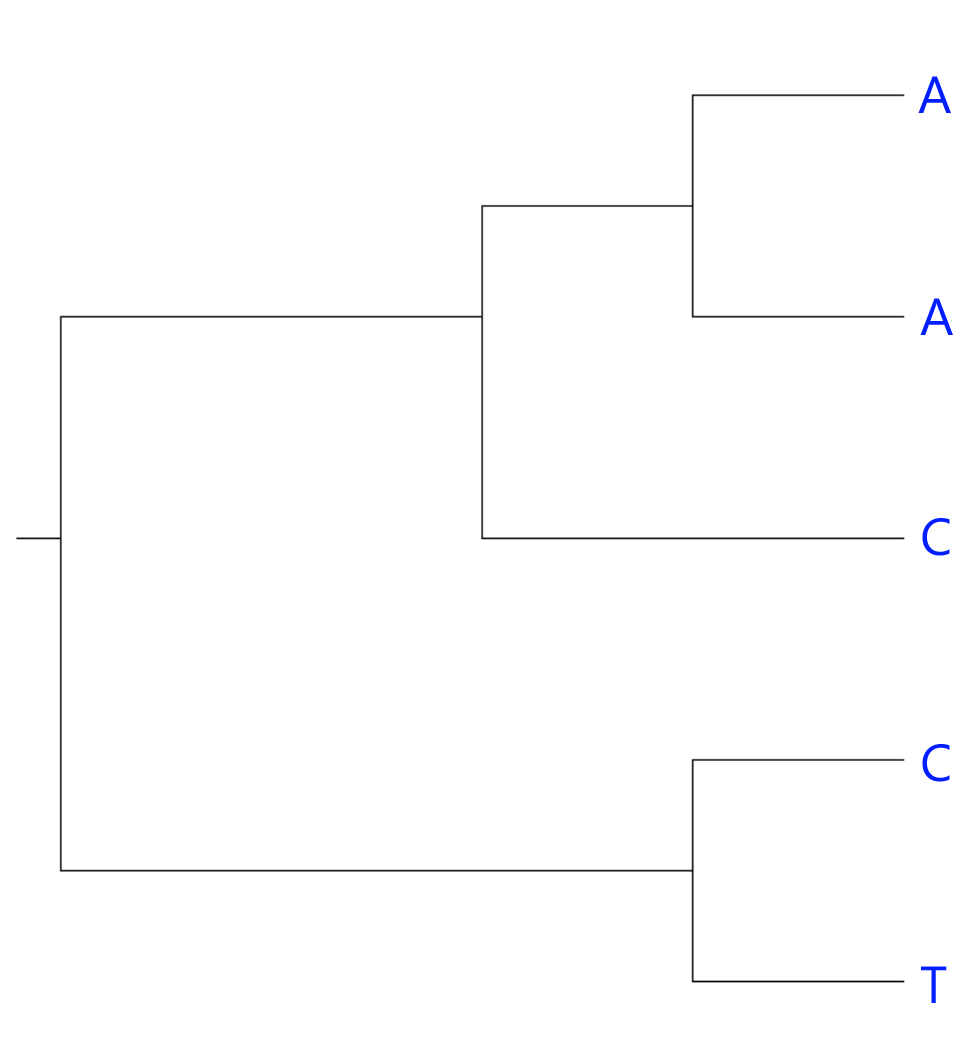
It's fairly obvious that our current hypothesis isn't optimal; the C's are not each other's closest relative. But for the sake of the example, let's try and figure this out the hard way.

Look at the two upper leaves. Both have A's so we can assume that their most recent common ancestor also had this base:

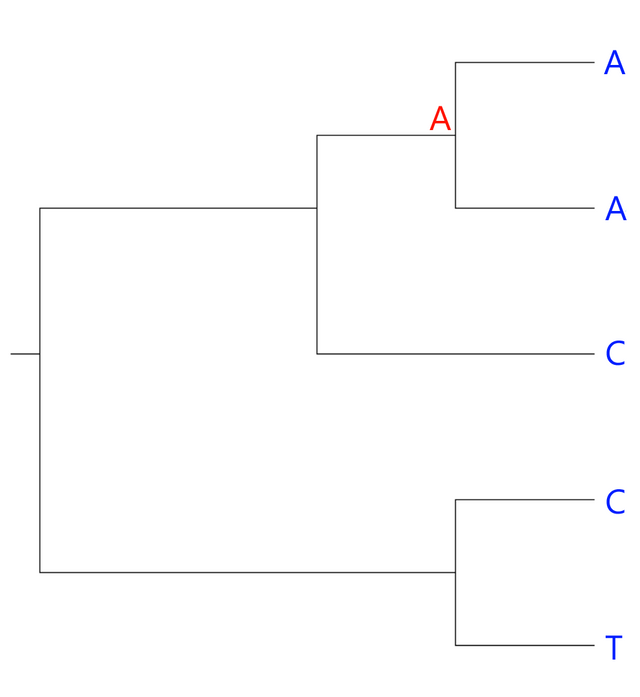
The two bottom leaves have different bases. Therefore, the ancestral character could be either a C or a T. Similarly, the ancestral node connecting the three upper leaves could have either an A or a C:

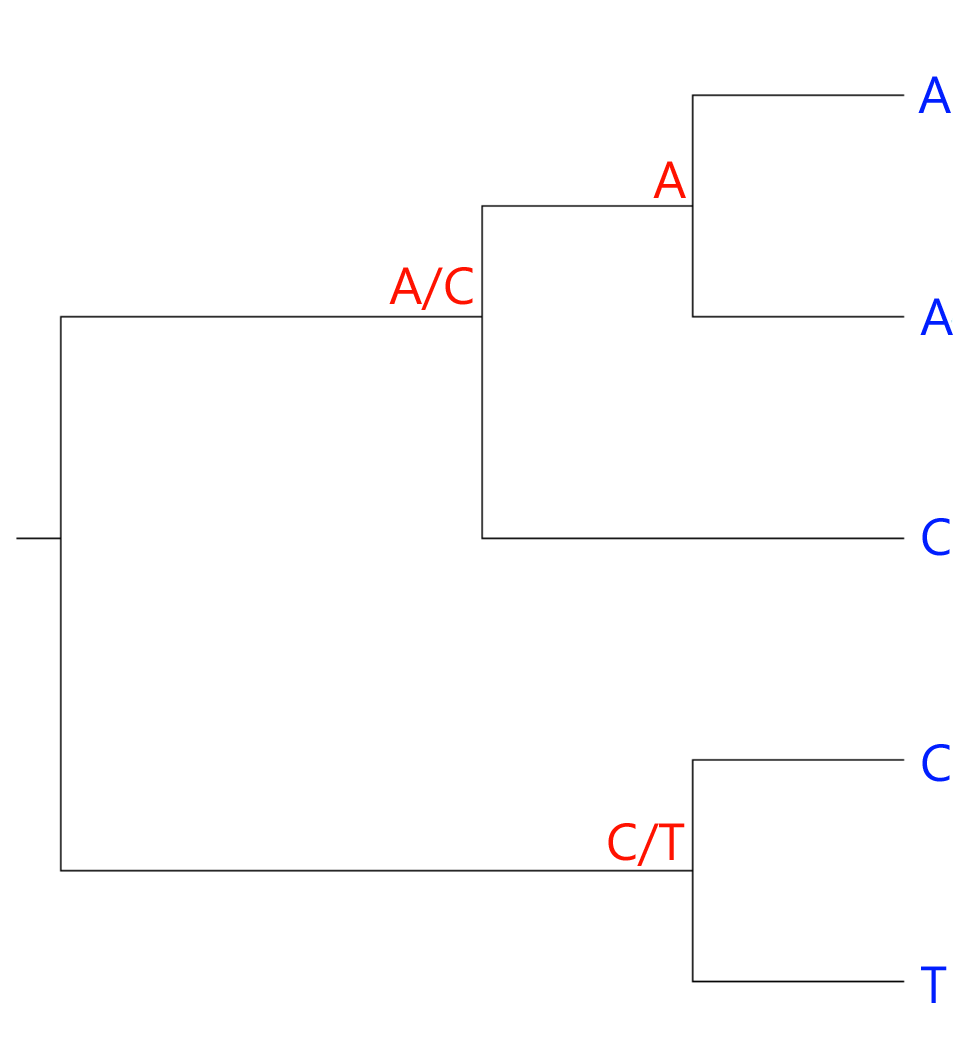
At the root of the tree, the character could be either an A, a C or a T. However, C was an option in both of the nodes following the root node, so we go with a C:

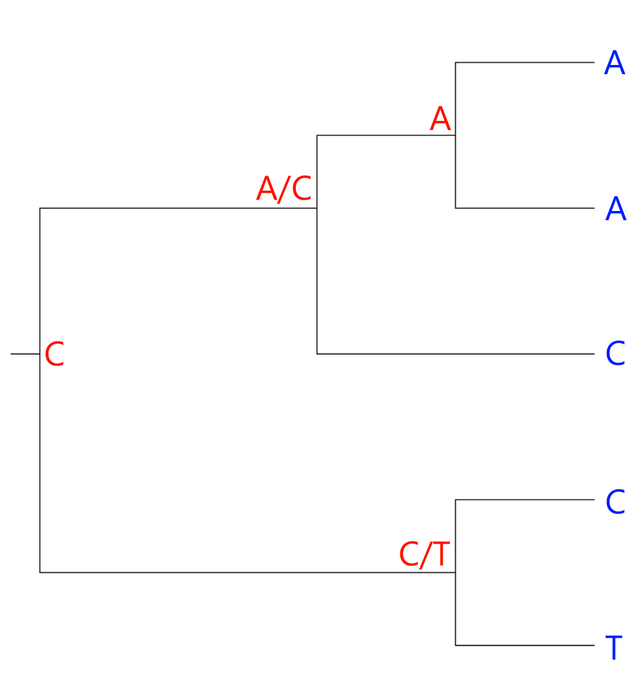
The number of ambiguous nodes, two, is the number of changes we have to assume to arrive at our current hypothetical tree. Curiously, this is actually the same number we would arrive at, had our hypothesis grouped the A's as sister taxa and the C's as sister taxa:

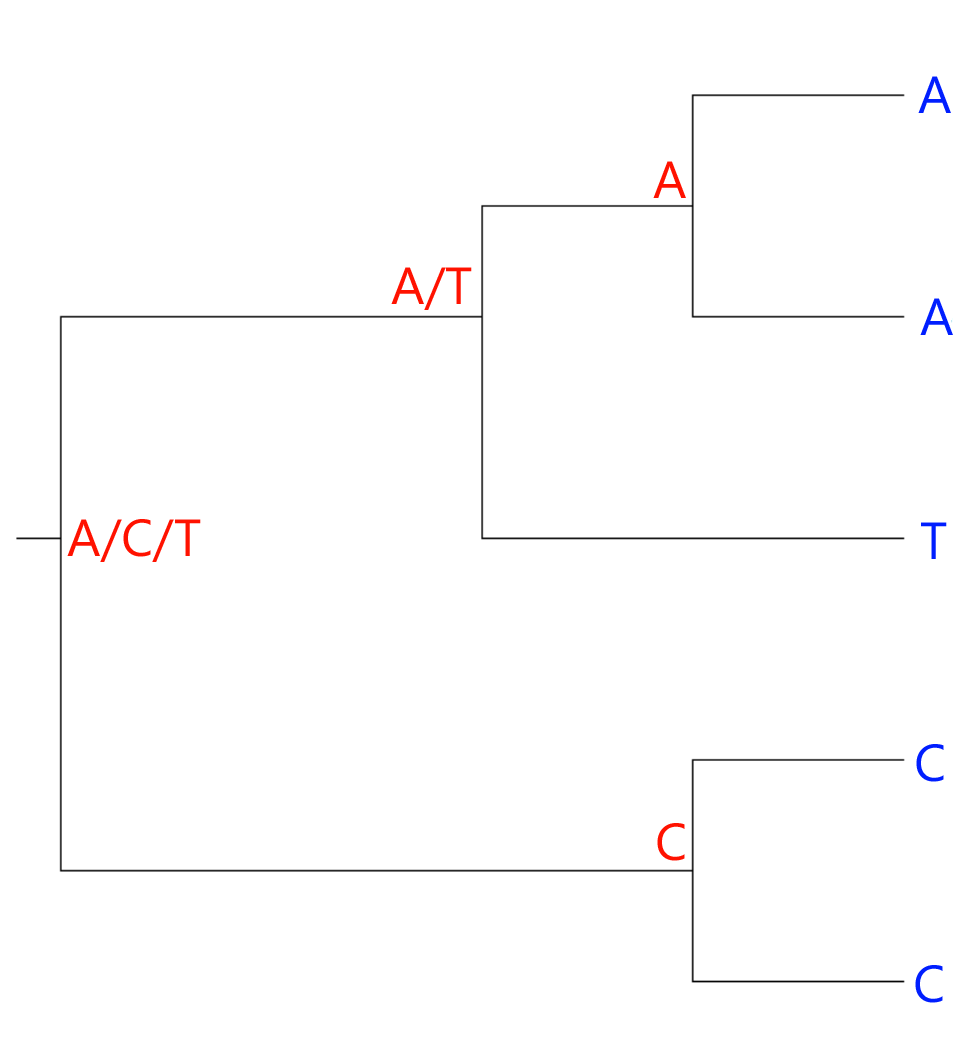
Thus, in this very simplistic example, we don't have enough information to single out the best solution by maximum parsimony. In practice, this would not be a problem, because you would never apply maximum parsimony unless you had more than a single trait to use for comparisons.

Book reference

Marketa Zvelebil and Jeremy O. Baum (2008): "Understanding Bioinformatics"

Tree-drawing tool

http://iubio.bio.indiana.edu/treeapp/treeprint-form.html