Introduction
Bose-Einstein condensates, are in my opinion some of the most amazing, and awe-inspiring phenomena that we, as a species are aware of. Their bizarre and recondite properties are direct results of quantum mechanics. In essence, they are macroscopic quantum phenomena, and can only be observed at very low temperatures. The principal discoveries have taken place over the course of a hundred years, starting in the early years of the twentieth century and still continuing with great pace, to this day!
The field of low temperature physics can be said to have had its beginnings in 1908, when helium was first liquified at the laboratory of H. Hammerling Onnes in Leiden, The Netherlands. It wasn't terribly along afterwards when superconductivity was discovered in the same laboratory! Despite this long history, research into these states of matter is still developing, and has been completely revolutionised with novel discoveries in recent years. Over the years we have progressed to study systens at lower and lower temperatures, with the current cutting edge characterised by the study of atomic BEC at nano-Kelvin temperatures.
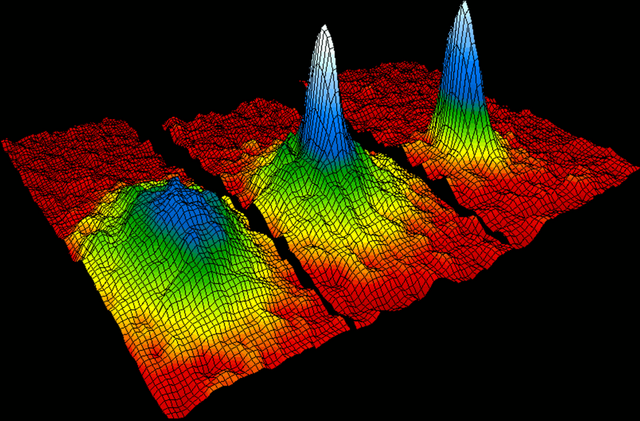
Successive occurrence of Bose-Einstein condensation in rubidium. From left to right is shown the atomic distribution in the cloud just prior to condensation, at the start of condensation and after full condensation. High peaks correspond to a large number of atoms. Silhouettes of the expanding atom cloud were recorded 6 ms after switching off the confining forces of the atom trap.
[ source/image credit ]
Historical perspective
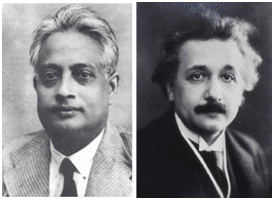 |
In 1924, Bose wrote to Einstein describing his new method to derive the Planck black-body formula. At that time Einstein was already a superstar, having just won the Nobel prize for his groundbreaking work on the photoelectric effect. |
Bose was a relatively unknown scientist, at the time, working in Bangladesh (then, Dacca). His previous letters to European journals had been ignored, but Einstein saw the potential in his novel ideas and helped him to publish the results.
The idea that Bose introduced was to treat the electromagnetic waves of the block-body as a gas of identical particles. This was the first time that the spooky light quanta (introduced by Planck and Einstein to account for the photoelectric effect) could be thought of as particles! Yes - particles of light; we now refer to them as photons!
Einstein extended these ideas to the regime of an ideal gas of particles, with non-zero mass. This was the first fully fledged quantum mechanical generalisation of the standard classical theory of the ideal gas. We know now that there are two distinct quantum ideal gases, corresponding to either Bose-Einstein or Fermi-Dirac statistics. The method of counting quantum states introduced by Bose and Einstein applies to boson particles, such as photons or 4He atoms. The main idea, here, is that for identical quantum particles, we can simply count the number of available quantum states using combinatorics.
Bose-Einstein statistics
If we have Ns identical Bose particles in Ms available quantum states then there are
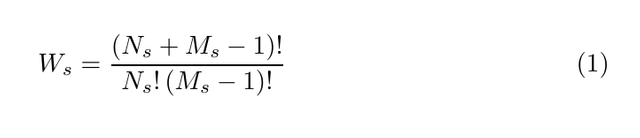
available ways that the particles can be distributed. Now, we apply this combinatoric rule to the thermodynamics of an ideal gas of N boson particles which are occupying some volume V. Using periodic boundary conditions, it is the case that any individual atom will be in a plane-wave quantum state,

where the allowed wave vectors are
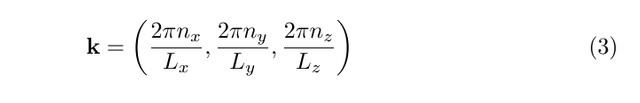
and where Lx, Ly, and Lz are the lengths of the volume in the x, y and z directions. The total volume is given by V = LxLyLz, and thus an infinitesimal volume d3k = dkxdkydkz of k-space contains

quantum states. Each of these single particle quantum states has an energy

where m is the particle mass. The next step is a clever trick of dividing up the available single particle quantum states into a number of thin spherical shells of states. By equation (5), a shell of radius ks and thickness δks contains
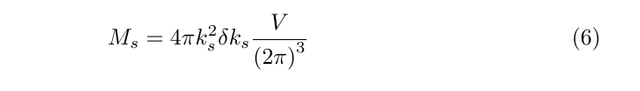
single particle states.
The number of available states between energy εs and εs + δεs is therefore
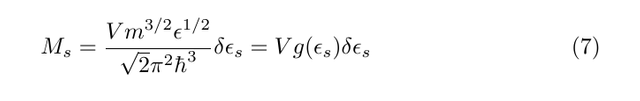
where g(ε) is the density of states per unit volume. We know from the fundamentals of statistical mechanics that the total entropy of the gas is given by S = kB ln W, where kB is Boltzmann's constant and W is the number of available microstates of a given total energy E. Using the Stirling approximation, and writing the total number of available microstates for the whole gas as the product of the number of available states in each k-space shell, it is possible to show that the number of particles in each energy shell, Ns, is given by
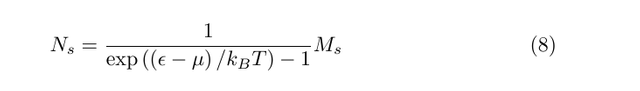
Now, the average number of particles occupying any single quantum state is Ns/Ms, so the average occupation number of any given single particle state of energy εk is given by the Bose-Einstein distribution
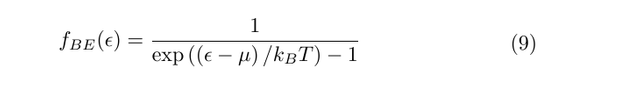
Over the course of the next few posts on BECs, we will examine the consequences of this result, and consider BEC in ultra-cold atomic gases. Cheers, D.
Very informative!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Very interesting your article, nice job. Have a nice day.
I follow u, follow me back if u want lot of fun and amazing picture every day.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @diracdnb! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honnor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBy upvoting this notification, you can help all Steemit users. Learn how here!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit