Feynman diagrams are an ingenious way of describing particle interactions; that is, events in which two particles come speeding towards each other and then smash apart! What we have just crudely described is what is known in physics as a scattering process. The idea is simple, but the implications are utterly staggering.

In general, we know what the incoming particles are – they could be electrons, muons, neutrinos, photons, and so on, and so forth. This is what is referred to as the ‘in state’. We can also detect the final particles that come out of this interaction, that manifest in the ‘end state’. But what goes on in between? This is called the interaction, and when Feynman pioneered this idea he was studying the interactions between electrons, anti-electrons (positrons) and light – photons. There’s a special name given to the study of these systems: quantum electrodynamics, or QED for short.
|
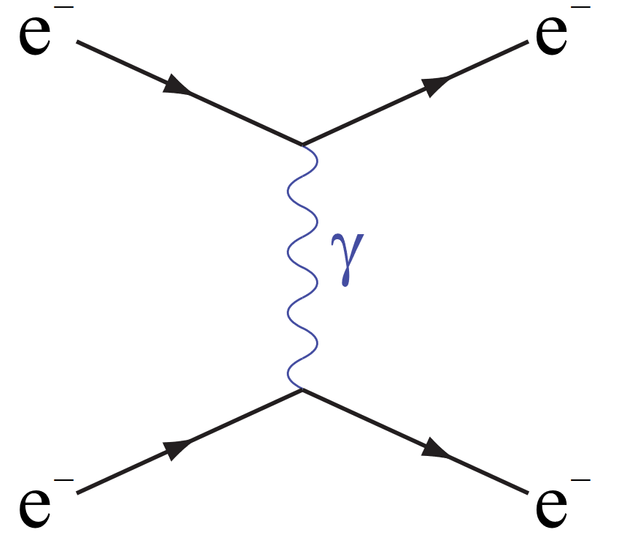
Now, suppose we have two electrons, which are racing towards one another. Something rather strange happens between them – a photon is emitted by one, and absorbed by the other as they move apart! This is represented by the squiggly line in the diagram. |
This is Feynman’s version of the notion of a Coulomb repulsion between the two electrons as they move together (but don’t completely touch!) and are repelled. Feynman came up with this pictorial representation because these particle interactions turn out to be a little more subtle than you might at first anticipate. There are many, many ways the interaction can pan out!
|
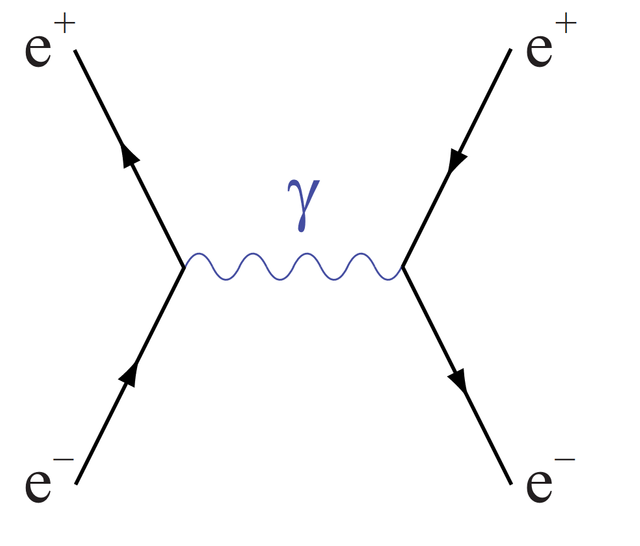
Lets now suppose that we have an electron and a positron that are moving through time, and on a collision course in space. The positron is the electron’s arch enemy (read: its antiparticle), and wants nothing more than to annihilate with it! |
|
When these two particles come together, with equal and opposite momentum, we get as the end state just pure energy in the form of photons. The story doesn’t end there, though – there’s nothing stopping this energy being taken away through the production of, say, a muon and anti-muon pair, for example.
The tremendous power of Feynman diagrams are most appreciated when working about all the possible combinations of the particles which will lead to some given end-state.
One way to think about all these different particle combinations is by thinking about an ant colony. Most of the ants travel along the much loved ‘big stick’, carrying leaves, and so on. They’re just trying to get from A to B. Maybe the much fabled big stick gets crowded, and a subset of ants start travelling along less obvious, smaller sticks on their way from A to B. We know the start point (A) and we know the end-point (B), but the individual paths of the ants can be different. Some paths, such as the ‘big stick highway’ are more probable than others. You can give a weighting, or probability to each of these paths, which is exactly what Feynman diagrams do in the case of particle interactions.
|
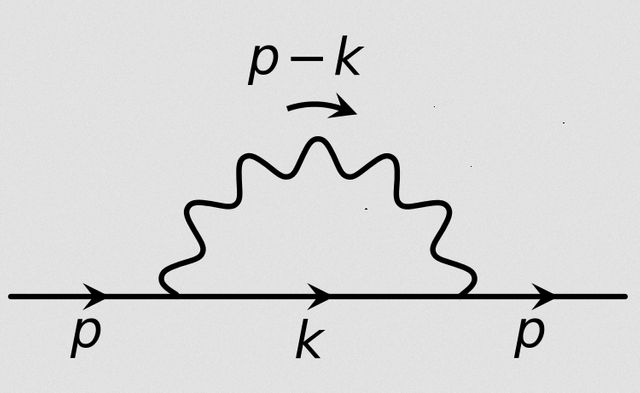
Lets consider a different situation now - suppose we just have a single electron traveling forward in time. There is a non-zero probability that it can emit a photon and reabsorb it. Maybe it does it a second, or third time. |
|
The picture we end up with is the electron carrying along with it a cloud of virtual photons, which fluctuate around it. This is interpreted as a so-called, self-energy correction and it effects the mass of particles.
Feynman turned these diagrams into a mathematical language; namely, QED, which is shockingly accurate – in fact, the most accurate theory we have in physics!
When you’re actually dealing with Feynman diagrams in elementary particle physics calculations - like the kind of stuff they do at CERN or Fermilab - perhaps trying to determine the masses of particles or coupling strengths, it is necessary to take into account all the possible combinations of interactions (sticks, smaller sticks) that get you from A to B. This is called the sum over paths, or path integral formulation, and is a cornerstone of modern particle physics.
Nicely explained. thanks! Are you working in this field?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Very good summary, @diracdnb. Thanks a lot for bringing more science to Steemit. :-)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for the effort to provide people value. Your easy explanation is really grat. You have a new follower. I will appriciate it if you follow and upvote me too :))
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Very useful information!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
upvote make sure follow me and upvote my post if you like
https://steemit.com/steemit/@vegeto/steemit-for-beginners-upvoting-strategy
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Steemit needs more serious folk like yourself. Followed! Can't upvote tho cos I got low SP! )
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit