Hola amigos de Steemit, hoy quiero traerles un nuevo post relacionado con el contenido de mi tesis de grado.
Hoy les traigo: ¿Cómo determinar si un material es un sólido cristalino estudiando su nomenclatura?

Los materiales sólidos pueden clasificarse en cristalinos y amorfos, según la periodicidad geométrica del ordenamiento de los átomos o moléculas que lo componen.
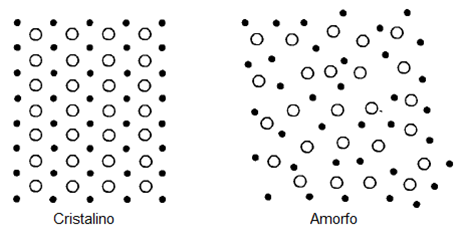
En los materiales amorfos, los átomos y moléculas pueden estar enlazados con bastante firmeza entre sí, pero poseen poca o ninguna regularidad o periodicidad geométrica, en la forma en que los átomos están acomodados en el espacio. Por otro lado, los cristalinos se caracterizan por tener una periodicidad perfecta (o casi perfecta) en su estructura atómica; esta regularidad de estructura proporciona un concepto muy simple de un cristal y facilita la tarea de comprender y calcular sus propiedades físicas (figura 1).
En una primera aproximación para saber si un sólido es un cristal se procede a los cálculos ab-initio, procedentes de la estructura de bandas. Que nos dice, que existen elementos que por naturaleza son cristalinos, los pertenecientes al grupo IV de la tabla periódica, ya que poseen una estructura tetraédrica con enlaces covalentes. Por esta razón, se ha seguido primeramente como una regla que un material con estructura tetraédrica que tenga enlaces covalentes, sea en primera hipótesis un sólido cristalino, es decir, los materiales que tengan 4 electrones de valencia disponibles en la última capa electrónica. Esto significa que no solo serán los elementos pertenecientes al grupo IV, sino que además, serán cristales los que cumplan la siguiente relación:
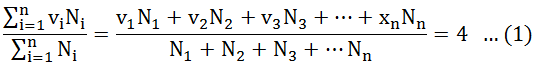
Donde N es el número de átomos de algún elemento que compone al material, v es el número de los electrones de valencia de dicho elemento, y la sumatoria se desarrolla con n igual al número total de elementos que componen al material. Esta relación se conoce como la Regla de Pamplin.
La existencia de la relación de Pamplin implica que además de los cristales formados por la unión de átomos del grupo IV, también se formaran cristales por la combinación de elementos de dos o más grupos diferentes, dando origen a los cristales binarios, ternarios, cuaternarios, etc. Po lo que existe una cantidad infinita de combinaciones posibles para la formación de un material cristalino, a través de la unión sistematizada de elementos de diferentes grupos.
Demostración:
Ahora demostraremos, con la ayuda de la tabla periódica (figura 2), que los compuestos binarios III-V y II-V, son cristalinos.

Para el binario (n=2) GaAs, perteneciente a la familia III-V, con valencias de Ga=3 y As=5, tenemos de la ecuación (1) que,
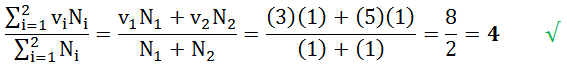
Y para el binario (n=2) ZnSe, pertenecientes a la familia II-VI, con valencias de Zn=2 y Se=6, de manera similar con la ecuación (1) que,
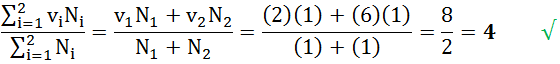
En mi Tesis...
En mi tesis el material estudiado es el ternario (n=3) Ag2PbTe3, perteneciente a la familia I2-IV-VI3, con valencias de Ag=1, Pb=4 y Te=6, por lo que usando (1),
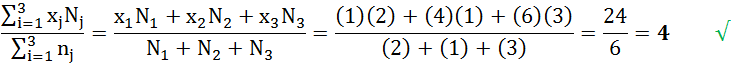
Demostrando teóricamente, que mi material es un sólido cristalino.
Gracias amigos, espero que sea grato para ustedes el conocimiento compartido.
Att. @djredimi2
Otra publicación relacionada:
Ciencia de los Materiales. ¿Cómo calcular la masa de los elementos que constituyen un material?
Muy interesante tu post. Excelente!. Gracias por compartirlo :-D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por su comentario Profesor, es un gustaso verlo por acá. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Interesante @djredimi2 ¿estudias quimica? pasa por mi blog, hay material interesante. Ademas quiero pedirte un favor, vota por mi en este concurso de ante mano gracias. https://steemit.com/spanish/@skynov/concurso-cervantes-xa-entrega-gloria-fuertes-la-linea-intermedia te sigo y te deje mi voto 👍
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @skynov estudio física pura. Claro que si estaré pasándome por tu blog. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit