Hello everyone, in this opportunity, I want to talk about the Taylor series
Many of us have come across limit, derivative, and/or integral calculus of complicated functions. Taylor's theorem is named after the British mathematician Brook Taylor. This theorem allows us to approximate any function through a polynomial, so the above calculations are simpler in this type of function.
(Taylor Series) Let f be a real or complex function infinitely differentiable at the point x = a then the Taylor series of f (x) centered on a is:
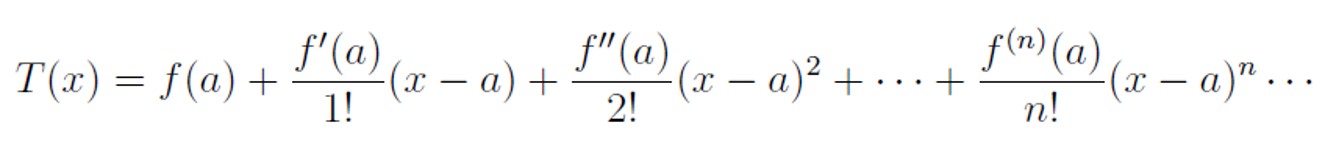
Note that T (x) is the only polynomial that satisfies:
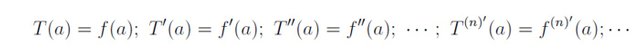
- Example: The Taylor polynomial of order six, eight and ten for f (x) = sin (x) / x centered at x = 0 is:*
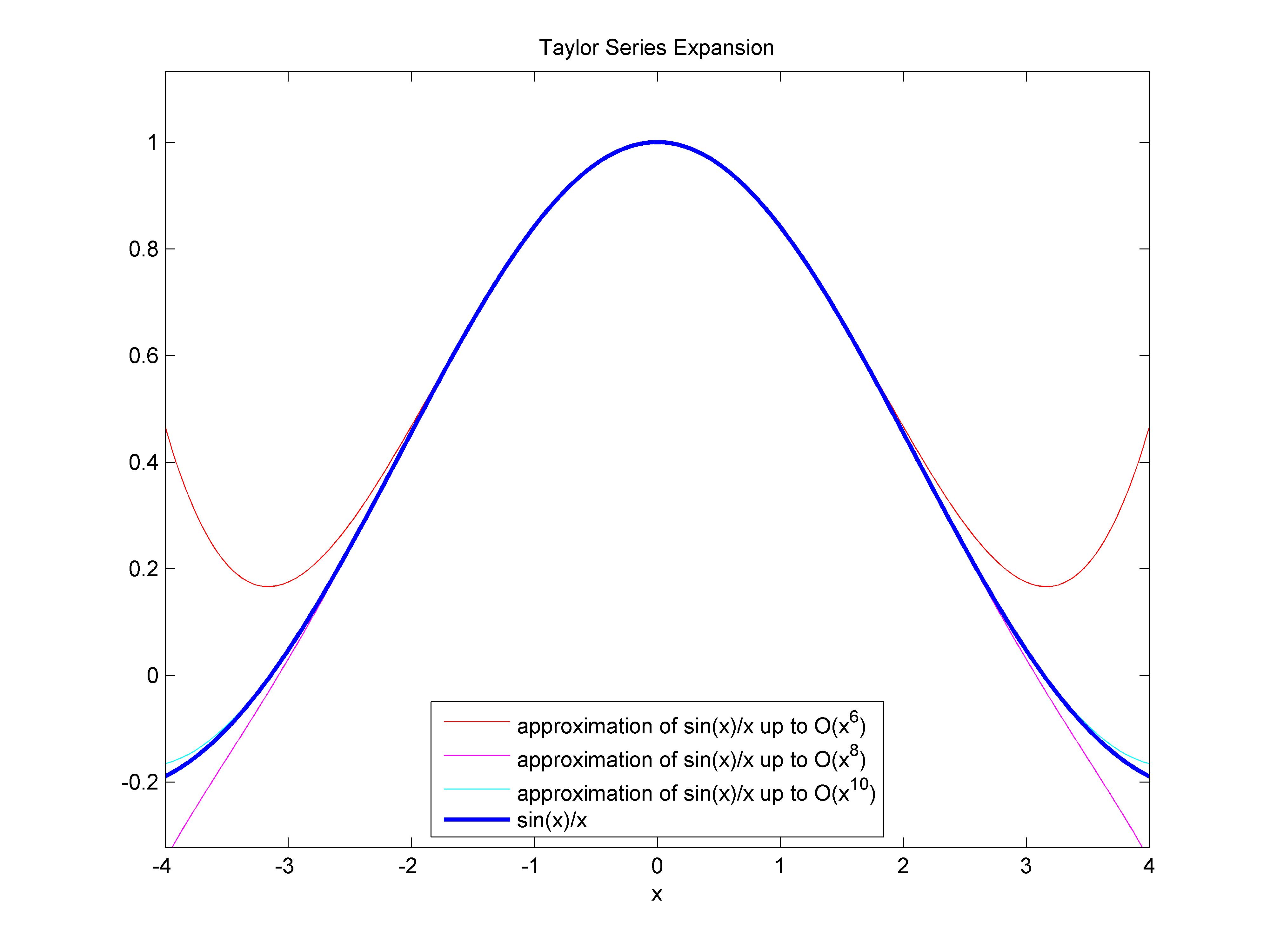
Notes that the higher the order of the polynomial the better the approximation
enjoy and upvote, follow me @falcao12
Nice job. Are you able to embed the latex in there or are those images?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks, they are images, it would be wonderful to be able to write in latex here
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit