Hello to the beautiful scientific community of steemit, this time I want to introduce one of my undergraduate theses, basically we work with a non-deterministic epidemiological model using real data, the model can be found in several bibliographies, but one our case was tested with real data getting wonderful results:
This model is for an epidemic consisting of susceptible and infected subpopulations. Consider a SIS epidemic model for a single species. In this model, susceptibles become infected, recover, and become susceptible again. There is no immunity to the disease.
dS/dt=γI−αIS/N
dI/dt=−γI+αIS/N
where S(0)+I(0) =N and therefore S(t)+I(t)=N fort≥0. In this model, S(t) is the susceptible population size, I(t) is the infected population size,α>0 is the contact rate for passing the infection, i.e., the average number of individuals with whom an infected individual makes sufficient contact to pass an infection, and γ>0 is the probability that an infected individual is removed from the infection process during a unit time interval (relative removal rate).
In terms of the parameters dened in the rst subsection,
x1(t)=S(t), x2(t)=I(t), d1=d2=b1=b2=0,
m12=αI/(I+S)=αx2/(x1+x2), and m21=γ.
The stochastic SIS model has the form
dx1=(−m12x1+m21x2)dt+sqrt(m12x1+m21x2)(dW1−dW2)
dx2=(m12x1−m21x2)dt+sqrt(m12x1+m21x2)(-dW1+dW2))
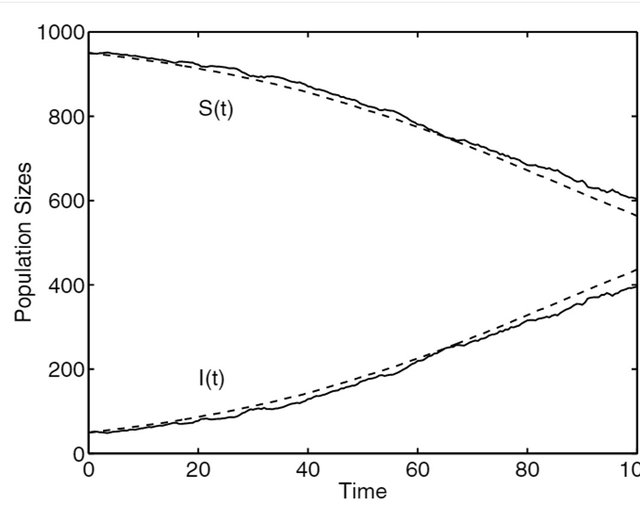
In this picture, we can see expected population sizes (dashed lines) and one sample path for susceptible and infected
enjoy, resteem and follow me @falcao12