Preamble: After not having time to write a proper science-related article for a while, I decided today that it's time to write one again. Today's topic: Elasticity. One word of warning though: I'm not a physicist. Thus, please let me know if I mixed up some physics-lingo or expressed myself inaccurately at some point.

Elasticity

Elasticity is defined as the ability of a body to resist a distorting influence or stress and to return to its original size and shape when the stress is removed. Fluids resist a change in volume, but not in shape and thus possess only volume elasticity. Solids resist changes in shape and volume (to a certain extent) and thus possess rigidity or shear elasticity, as well as volume elasticity. In order to measure elasticity, three different physical moduli can be distinguished: Young’s modulus, shear modulus and bulk modulus.

Young’s modulus

The modulus measuring longitudinal elasticity is called Young’s modulus E and was named after the English mathematician and physician Thomas Young (1773 - 1829). It is defined as the ratio between stress and strain. In this context stress is defined as force F over area A (i.e.
F / A) and is measured in Pascal (i.e. P a = N / m^2 ). Strain is defined as the change in size deltaX over the size (or height) of a certain material. To illustrate this concept vividly, one might consider a block made of a certain material (e.g. some kind of gel) which is being "shifted" by applying an external force to the surface of this block. The strain is then given as the ratio of the resulting shift deltaX over the height h of the block. A visualization of this example is given below:

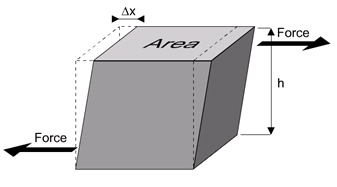
Source: http://www.spaceflight.esa.int/

The dependence of the Young’s modulus on different tissue types makes it a very important measure to determine tissue hardness or stiffness. The harder a certain material is, the larger the measured Young’s modulus will be. Traditional palpation measurements are based exclusively on sensing the variations of the Young’s modulus of tissue [1].

According to [1], the published data concerning elasticity measurements for different tissues are often of limited use only (as of 2011). Even for tissues of the same type, discrepancies between the published values can be found. Some of these discrepancies may have been caused by the indiscriminate treatment of large strains in Lagrangian or Eulerian representations. In Lagrangian representations, the data is given relative to the original length and in Eulerian representations, the data is given relative to the strained length [2].

Shear modulus

The shear modulus or torsion modulus μ is a measure of rigidity and always has a value >= 0. It describes the material’s response to shear stress. The viscoelasticity of a certain tissue is only dependent on the shear modulus. A small shear modulus value indicates a less rigid material. Thus, a liquid can be defined as a material that has a shear modulus value of zero. Similar to the Young’s modulus, its unit is also Pascal (i.e. N / m^2). Under some assumptions the shear modulus can be deduced from the Young’s modulus (and vice versa) through the following relation [3]: μ = E / 3

This relation only holds for homogeneous and isotropic soft tissue (i.e. tissue with the same mechanical properties in all directions) and not for anisotropic tissue (i.e. tissue with different mechanical properties in different directions). An example for anisotropic tissue is muscle tissue, as this kind of tissue consists of fibres exerting forces in various directions. Even tough the equation above does not hold for all kinds of soft tissues, it is still used in many clinical scenarios because it has proven to be a valid simplification for most tissue types [3]. The shear modulus μ is defined as: μ = p * c^2,
where p is the density of the medium and c is the shear wave speed. Thus, the equation above can be rewritten as follows: p * c^2 = E / 3 <=> E = 3 * p * c^2

Hence, it becomes a trivial endeavour to compute the Young’s modulus of a given tissue, once its density p and shear wave speed c are known.

Bulk modulus

The bulk or volume modulus K measures the resistance of a material to uniform compression. Uniform compression means that an equal compressional force coming from all directions at the same time is applied to the material (see below).

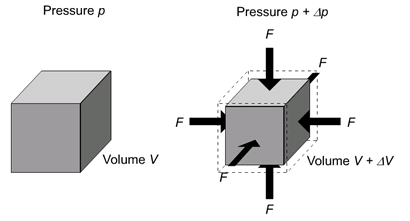
Source: http://www.spaceflight.esa.int/

The bulk modulus can be seen as an indicator for volume elasticity. In contrast to shear elasticity, the bulk modulus depends on short range molecular interactions and is defined mainly by the molecular composition of the examined tissue. Soft tissues can be called "incompressible" because they are constrained to undergo volume-preserving deformations and motions. In other words, soft tissues always attempt to preserve their volume and fill "gaps" within the body if exposed to some external pressure. This effect has been known since Jan Swammerdam, a Dutch biologist and microscopist (1637 - 1680), showed that muscles do not change volume on contraction in 1667 [4]. In general, the bulk moduli of soft tissues are several orders of magnitude larger than their corresponding shear moduli. The reason for that is the fact that water is a substantial part of soft tissue and its bulk modulus is very close to the bulk modulus of water, varying about 10 % only [1].

Interrelation of different moduli

All the moduli described above are physically interrelated. This interrelation makes use of one additional parameter, called Poisson’s ratio. This ratio is named after the French mathematician, geometer, and physicist Siméon Denis Poisson (1781 - 1840) and defined as follows [1]:

p_ratio = (lateral contraction per unit breadth / longitudinal extension per unit length).

Using the Poisson’s ratio, the following relations between the Young’s modulus E, the shear modulus μ and the bulk modulus K can be established [1] [5]:

• μ = E / 2(1+p_ratio)
• p_ratio = E / 2μ -1
• K = E / 3(1 - 2 * p_ratio)

Summary and TL;DR

This article gave a rough overview over different physical moduli and their interrelation. Thank you very much for reading. Here is your reward:

Source: https://s-media-cache-ak0.pinimg.com/

References

• [1]: Armen Sarvazyan et al. “An overview of elastography–an emerging branch of medical
  imaging”. In: Current medical imaging reviews 7.4 (2011), p. 255.
• [2]: James F Price. “Lagrangian and eulerian representations of fluid flow: Kinematics and
  the equations of motion”. In: Woods Hole Oceanographic Institution, Woods Hole, MA 2543
  (2006).
• [3]: Jeremy Bercoff, Mickäel Tanter, and Mathias Fink. “Supersonic shear imaging: a new
  technique for soft tissue elasticity mapping”. In: Ultrasonics, Ferroelectrics, and Frequency
  Control, IEEE Transactions on 51.4 (2004), pp. 396–409.
• [4]: Matthew Cobb. “Exorcizing the animal spirits: Jan Swammerdam on nerve function”.
  In: Nature Reviews Neuroscience 3.5 (2002), pp. 395–400.
• [5]: Lev D Landau and EM Lifshitz. “Theory of Elasticity, vol. 7”. In: Course of Theoretical Physics 3 (1986), p. 109.