(Check the first part here)
First Steps Towards QM – Blackbody Radiation and the Quantum Hypothesis
Towards the end of the XIX century, a considerable amount of known physical phenomena was more or less well understood within a theoretical body which came to be known as Classical Physics. Newtonian mechanics was the foundational framework according to which any physical description should be conceived, with its concepts of space, time, motion, force and its three laws at the core of any other model. Thermodynamics complemented the description provided by Newtonian mechanics for systems in which heat transfers took place, and it found theoretical basis on the kinetic theory of gases and on the statistics of many particle systems, both essentially ruled at the microscopic level by Newtonian laws. Maxwell’s theory of electromagnetism further extended the kinds of interactions which could be taken into account in the physical description of systems, but always having Newtonian principles at its core as well. And everything seemed to fit nice and smoothly within this framework, with but a few technical issues to improve and loose ends to tie.

(Source)
It was only natural that any new phenomenon would motivate physicists’ attempts to describe them within this well-established theoretical body, most of the time very successfully. However, technological and experimental developments were also starting to probe nature in ways and at scales which had been inaccessible until then, and soon they would start revealing some phenomena which didn’t quite fit in like the vast majority of what was known by then. These challenges would progressively lead physicists to realize the need for a whole new theoretical framework which would be compatible with these new observations. One of the first and most important of these challenges was the study of blackbody radiation, which I will attempt to describe in the rest of this article.
All bodies are known to emit electromagnetic radiation to some degree which may vary according to that body’s composition, shape and surroundings. This is not a supposition, but an observable phenomenon which is qualitatively consistent with classical physics. The most common form of radiation emission, and incidentally the one which concerns us right now, is called thermal radiation, i.e. radiation that is originated by the conversion of a body’s thermal energy into electromagnetic energy. Temperature is a measure of the thermal energy of a body, so that thermal radiation is actually a slow cooling process through which a body dissipates some of its internal energy. As the body cools down and its temperature lowers, the character of the emitted radiation varies. Similarly, if we heat up the body, its thermal radiation changes as well. To put it simply, thermal radiation is directly related to the temperature of the emitting body. Thermal radiation usually ranges from the infrared to the ultraviolet regions of the electromagnetic spectrum.
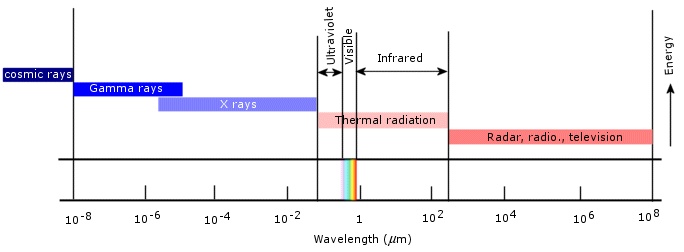
(Source)
A very useful approach to the study of some new phenomenon and to the development of a model is to consider an idealized system whose properties are analytically tractable. Once we have treated this problem, it is often a matter of properly parameterizing deviation from ideal behaviour in order to apply the ideas to real physical systems. This is especially useful if one can identify actual physical systems whose behaviour is sufficiently close to that of the idealized system, so that the model can be readily put to test within a relatively small error margin. Also, this idealized model ought to be built in a way which incorporates reasonable hypotheses regarding the essential physical mechanisms underlying the actual phenomenon. If the model then makes unreasonable or nonsensical predictions, this constitutes a strong motivation to reassess the hypotheses.
With this in mind, we are led to the definition of a blackbody, the concept of which has arisen within the study of thermal radiation and was originally introduced by Kirchhoff in 1860. A blackbody is an idealized object which absorbs all incident electromagnetic radiation. In order to have a clearer picture, you should be aware of what can happen to radiation upon impinging onto a body: 1) part of this radiation can be reflected, which means it scatters at its surface without interacting with its internal structure; 2) part can be absorbed, which means that it gets “consumed” inside the body, adding to its internal energy; 3) and part can be transmitted, which means that some of the radiation actually traverses the body, possibly interacting along its way with the body’s constituents until it eventually escapes the body again. So, a blackbody would be one which does not reflect nor transmit any portion of the incident radiation, absorbing all of it. This makes it a much simpler system to study, since a lot of possible phenomena which would complicate the analysis is altogether absent. Furthermore, being a perfect radiation absorber, a blackbody is also a perfect emitter, and it has become the standard in relation to which thermal radiation from physical bodies is usually characterized.
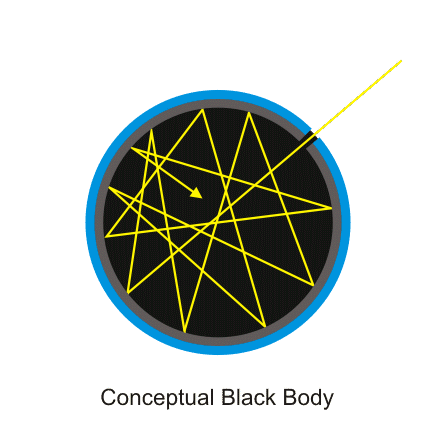
(Source)
We come then to the subject of blackbody radiation, which we are now in a position to define in an understandable way: it is the thermal radiation of a blackbody which is at thermal equilibrium, i.e. at constant temperature. As is the case for any specific body, thermal radiation is not emitted in a single frequency, but is spread across a wide spectrum of frequencies which are all emitted with different intensities. So, to characterize thermal radiation is to describe this spectral profile of which frequencies are emitted with which intensity. Owing to the idealized characteristics of a blackbody, the form of its thermal emission spectrum is a function of its temperature only, in such a way that if we knew exactly the relation between the form of the spectrum and the temperature, we would be able to measure temperature by simply looking at its emission spectrum. In fact, this technique is used to define effective temperatures of stars by measuring the radiation which they emit. Of course, stars are not perfect blackbodies, but still the estimate is reasonable and informative.
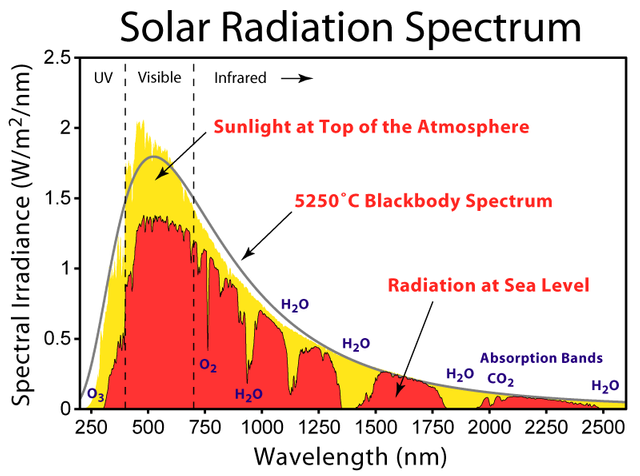
(Source)
Modelling of the thermal emission of a blackbody was initially carried out using assumptions and reasoning in accordance with classical statistical mechanics, namely the equipartition theorem. Very roughly, this theorem states that, in a system with many degrees of freedom at thermal equilibrium, all contribute the same average energy. A physical model of a blackbody at thermal equilibrium may be conceived as a cavity within which electromagnetic radiation is constantly emitted and absorbed in such a way that the overall temperature is kept constant. You may ponder for a bit and realize that this system satisfies the essential definition of a blackbody, i.e. it absorbs all incident radiation. Classical electromagnetic radiation, being a wavelike phenomenon, can be modelled within this cavity as a set of allowed oscillation modes which keep bouncing off its inner walls. Application of the equipartition theorem to such a system means that each possible mode of oscillation carries, on average, the same energy. Now, there are only a few low frequency modes which can be established, but as we consider higher and higher frequency modes, the number explodes, yielding the utterly absurd result that the total energy of the electromagnetic radiation within the cavity blows off to infinity. This nonsensical result, which has become known as the ultraviolet catastrophe, is expressed in the Rayleigh-Jeans law, the classical formula for the spectral profile of blackbody radiation.
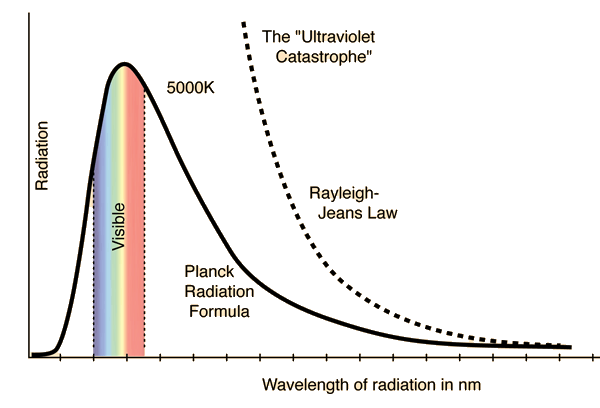
(Source)
The inconsistency of the classical result led Max Planck to rethink the assumptions employed in the classical calculation. He clearly identified the equipartition theorem as the main culprit behind the bad classical result, which allowed for any mode to be able to carry any energy value. In an attempt to resolve this issue, he suggested his famous quantum hypothesis, stating that the possible energies of each mode of oscillation are not continuously distributed, but rather quantized according to discrete energy levels given by the relation E = n h f, where n is any positive integer. What this formula means is that, for any frequency f, the total energy of modes oscillating at that frequency is an integer multiple of a fundamental quantum of energy which is proportional to the frequency f. The constant of proportionality, h, has since been called Planck’s constant, and it is ubiquitous throughout all of quantum physics.
Conceptually, his bold hypothesis implied that radiation could only be absorbed or emitted in discrete packets of definite energy, or quanta (later called photons by Einstein), a notion which was completely foreign to the classical description of radiation. This feature would later be related with atomic emission lines and motivate the development of the Bohr-Sommerfeld atomic model. The pragmatic consequence of such a hypothesis is that the energy was no longer equally distributed among all frequency modes, with higher frequencies getting severely suppressed to the point that, in the end, the total energy was finite and compatible with the values measured for actual physical systems whose behaviour was close to that of a blackbody. Planck’s law for the blackbody radiation was published in December of 1900, and his quantum hypothesis is considered the first breakthrough towards the development of quantum theory.

(Source)
On the basis of Planck's law, two other well-known and useful laws can be derived. One is the Stefan-Boltzmann law, which states the total power radiated by a blackbody per unit surface is proportional to the fourth power of the blackbody's temperature. Another one is Wien's displacement law, which tells us that the peak of the spectral profile of blackbody radiation occurs at a wavelength which is inversely proportional to its temperature. This is particularly useful for determining effective temperatures of stars, since all it takes then is to measure the peak wavelength and quickly compute the temperature using Wien's expression. All of these laws are in good agreement with experimental measurements of thermal radiation, in contrast with the classical Rayleigh-Jeans result. Planck's quantum hypothesis and the success of his calculation opened a door that would never again be closed.
Congratulations @jmorais! You have received a personal award!
Click on the badge to view your Board of Honor.
Do not miss the last announcement from @steemitboard!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @jmorais! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit