This is a French adaptation of my earlier post about special relativity and space travels.

[image credits: Pixabay]
A la demande d’@ixindamix, voici un article sur la relativité restreinte!
Comme l’univers est très vaste, on pourrait se demander si voyager jusqu’aux limites de ce dernier et en revenir (pour pouvoir dire à quiconque ce qui s’y trouve) est un rêve ou quelque chose de plutôt concret?
Est-ce qu’un simple et unique être humain pourrait y arriver (en l’espace de sa vie donc)?
C’est la question à laquelle je vais essayer de répondre de façon sérieuse dans cet article, à l’aide d’arguments de physique.
DISTANCE A PARCOURIR: TAILLE DE L’UNIVERS
Avant de démarrer un tel voyage, il est utile de se renseigner sur la distance à parcourir. Nous savons aujourd’hui que l’univers est vieux de 14 milliards d’années. Comme rien ne va plus vite que la lumière, on pourrait trivialement croire que la taille de l’univers est de 14 milliards d’années-lumière.
Cette estimation naïve est cependant erronée, car elle ignore le phénomène d’expansion de l’univers. Les calculs précis montrent en fait que l’univers serait plutôt d’une taille de 45 milliards d’années-lumière. Cela signifie 425.441.472.996.960.000.000.000 kilomètres.
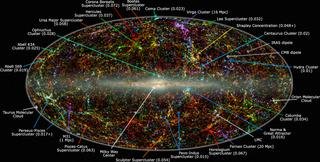
[image credits: IPAC / Caltech]
Nous avons donc à organiser un petit voyage de 850.882.945.993.920.000.000.000 pour l’aller-retour. Ca part mal…
En supposant que nous arrivions à voyager à la vitesse de la lumière, le voyage durerait 90 milliards d’années. Une bagatelle quoi. Un être humain aurait le temps de mourir quelques fois…
Mais en fait, c’est pire que cela. Au décollage, notre vaisseau spatial est au repos (à vitesse nulle quoi). Il faut donc qu’il accélère jusqu’à la vitesse de la lumière, et qu’à mi-chemin, il se mette à ralentir pour pouvoir s’arrêter pile à la fin de l’univers.
De façon plus pratique, à mi-chemin, le vaisseau va faire demi-tour et garder son accélération (mais à contre-sens). Cela va l’amener à ralentir tranquillement et s’arrêter pile à l’arrivée.
Ensuite, idem pour le trajet retour… Et oui, le voyage va prendre du temps…
LA RELATIVITE RESTREINTE A LA RESCOUSSE
Mais pour le moment, nous avons oublié un élément clé du calcul: la relativité restreinte. Einstein va nous sauver!

[image credits: Wikipedia]
Lorsque l’on voyage à haute vélocité, deux phénomènes ont lieu: la dilatation du temps et la contraction des longueurs.
En gros, le temps avance moins vite pour quelqu’un se mouvant à une vitesse proche de la vitesse de la lumière, et les distances paraissent plus petites.
Il reste à faire les calculs en prenant cela en compte.
Nous avons donc dit que nous partions de la Terre à vitesse nulle et que le vaisseau se mettait ensuite à accélérer. Très bien.
Mais nous ne pouvons accélérer n’importe comment vu que nous ne voulons pas tuer notre passager humain.
Nous allons donc imposer que l’accélération ne soit pas plus forte qu’1G. Pas trop de G dans la tronche de notre humain est une bonne chose! La gravité à bord sera donc identique à la gravité sur Terre.
On a à présent toutes les infos pour faire le calcul.
LE POINT DE VUE DE NOTRE AMI RESTE SUR TERRE
Comme mentionné plus haut, le voyage aller est un voyage de 425.441.472.996.960.000.000.000 kilomètres. Nous allons accélérer avec une accélération de 1G, puis faire demi-tour à mi-chemin avant de s’arrêter pile aux confins de l’univers.
Cela veut donc dire qu’il nous faut planifier un voyage de 212.720.736.498.480.000.000.000 kilomètres, en démarrant d’une vitesse nulle et avec une accélération constante de 1G. Oui je sais je radote…
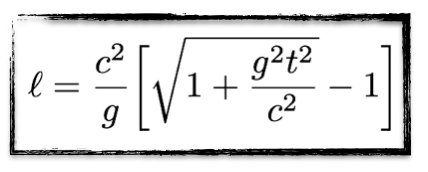
[image credits: homemade]
Pour quelqu’un resté sur Terre, le temps (t) que ce demi voyage de 212.720.736.498.480.000.000.000 kilomètres peut être calculé à l’aide de l’équation sur la droite.
Le l dans le membre de gauche est la distance à parcourir et g = 9.81 m/s2 est l’accélération correspondant à 1G. c est la vitesse de la lumière.
Facile à résoudre. Un crayon, une feuille de papier et on trouve un temps total pour l’aller simple de 45.000.000.000 années. A multiplier par deux pour l’aller-retour.
Zut, notre humain est mort, mort, mort et re-mort. (Des questions?)
En fait, la conclusion ci-dessus est erronée. Notre ami sur Terre est bien mort depuis fort longtemps. Pour le voyageur, nous n’avons pas effectué le bon calcul prenant correctement en compte les effets relativistes.
LE POINT DE VUE DU VOYAGEUR
Dans notre vaisseau relativiste, le temps s’écoule plus lentement=, comme nous l’avons dit ci-dessus. La formule ci-dessus doit donc être modifiée de façon appropriée.
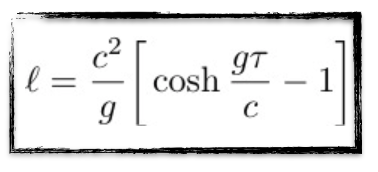
[image credits: homemade]
Il faut en effet utiliser la formule ici à gauche. Le temps nécessaire pour le voyage (noté τ ce coup-ci) est alors le temps ressenti par le voyageur (et pas cela ressenti par son pote resté sur Terre).
Et c’est là que cela devient drôle. Le calcul nous donne un aller simple d’une durée de 47.5 années! Pour l’aller-retour, cela donne donc 95 ans.
Notre voyageur peut donc totalement survivre au voyage!
DISCUSSION ET REFERENCES
En principe, il est donc possible de se rendre aux confins de l’univers et de revenir, pourvu que l’on puisse construire un vaisseau capable d’atteindre des vitesses extrêmement proches de la vitesse de la lumière.
Si c’est le cas, il suffit de mettre un bébé dans un vaisseau, et l’on récupérera sur Terre, 90 milliards d’années plus tard, un vieillard de 95 ans. Y aura-t-il seulement encore une planète Terre à ce moment-là? Ouais… un petit détail ;)
Par contre, ce que j’ai sous-entendu est qu’il faudra maintenir une accélération constante de 1G pendant 95 ans. Cela prend, plus ou moins, une quantité infinie de carburant. Conclusion: il nous est impossible de voyager jusqu’aux limites de l’univers et de revenir sans développer de nouvelles technologies pour les voyages spatiaux.
Petit jeu: j’ai effectué une approximation dans mon raisonnement que je n’ai pas mentionnée. Quelle est-elle?
Plus d’informations sur la physique de cet article peuvent se trouver ici:
- L’âge de l’univers et sa taille (en anglais).
- Un livre en francais sur la relativité.
Pour toute discussion sur ce sujet (ou sur les sciences en général), ne pas hésiter à venir faire coucou sur le canal #steemSTEM du Steemit chat.
SteemSTEM est un projet destiné à promouvoir le contenu STEM (Science, Technologie, Ingénierie et Mathématiques) sur Steemit. Non seulement on vote et resteem pour les articles de qualité, mais on redistribue les gains sous forme de STEEM Power aux membres de la communauté de Steemians versés dans le science/technologie. Pour plus d’informations, voir ici (en anglais). Pour rejoindre notre trail de curation, contactez-nous sur le chat. Merci à l’avance pour votre support.
Nice posting @lemouth
This is very important for me
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
How it is important? Please tell me, I am curious ^^
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Einstein got the noble prize by publishing the Theory.
So there is a chance , if somebody study minutely,
he might get some PHD at-least.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well... I didn't get your comment. Do you mind clarifying? Thanks in advance! :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Wahou!!! Pour une fois que je comprends ce que tu racontes!!! Bon ok... j'avoue que j'ai un peu fait l'impasse sur les equations... moi et les membres de gauche et de droite, tu sais ce que j'en pense! :P
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Merci d'avoir répondu à ma requête et d'éclairer ainsi les zones d'ombres sur ce sujet qui me passionne tant. Cette question de voyages spatiaux et de sa problématique sur le temps qui s'écoule, provient, pour ma part, plus particulièrement d'une oeuvre qui m'a marqué et qui traitait de ce sujet. Il s'agit d'un anime se nommant Gunbuster, réalisé par le studio Gainax à la fin des années 80, ou le dénouement tragique mettait le doigt sur les conséquences de l'abus de déplacement dans le confin de l'univers (5cm Per Second, le fait parfaitement aussi). Je vous recommande chaudement le visionnage de cet oeuvre, qui apparemment est assez réaliste sur ce point.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Vraiment un article excellant, ça laisse à la fois songeur et rêveur :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Personnellement, je n'ai pas envie de passer ma vie entiere dans un vaisseau spatial. Donc je n'en reve pas trop ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Mon côté fana de Stargate Univers peut être... ^^'
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ahah! Jamais vu celui la. Me suis arrete aux opus precedents :p
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
waaaww.. It is true, steemit has a lot of teachers. science is overwhelming.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yes it is true ^^
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I followed the link to the English translation. That was an awesome work on Space travel and Relativity.
merci d'avoir partagé cela (you once taught me this. Hope I got it correctly?)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
It is totally correct ^^
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I guess my teacher will be proud of me :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
He is ^^
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Très très belle introduction à mon prochain article ^^
Merci et bravo :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
J'ai hate de lire ca :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Voila je l'ai lu. Joli article en effet :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Merci beaucoup ! On essaye toujours de faire au mieux et une fois publié on se dit toujours qu'on aurait pu faire mieux :)
Bonne semaine
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
chouette article!
J'ai étudié pas mal de sciences aussi et il me semble que tu aurais pu mentionner que la masse aussi devient plus grosse quand on approche la vitesse de la lumiere.
a par ça chapeau pour le raisonnement!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Merci pour ton commentaire.
Je ne suis pas d'accord avec toi, car c'est incorrect de dire cela. La masse est invariante. C'est une propriete intrinseque d'un objet. Quand on parle de 'masse relativiste' (j'ai horreur de ce terme qui ne veut pas dire grand chose stricto sensu), on parle en fait d'energie (donc autant appeler cela energie des le depart).
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Euh oui? Que veux-tu dire? :D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Plus rationnel et illustratif que tout oeuvre de science fiction ayant abordé le sujet. Upvoté à 100% !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Merci ^^ Oh, un nouvel avatar!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Enfin j'ai eu le temps de lire ton article correctement. Le moins que l'on puisse dire c'est que ça fait rêver, bien que la technologie pour y parvenir n'existe pas (encore), qui sait peut-être qu'un jour...
Pour l'approximation que nous devons trouver, ne serait ce pas une histoire d’expansion de l'univers? Car il me semble que ton calcul prend en compte les distances à l'instant T mais si l'univers est en perpétuel expansion la distance totale ne devrait-elle pas être plus grande que ces chiffres ?
Donc pendant le voyage, l'univers continue de grandir, donc plus de temps que prévu pour atteindre "la ligne d'arrivée" et pour le retour une distance encore plus grande ?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Honnetement, je reste tres sceptique concernant la technologie qui permettra de faire cela, en raison de la quantite de combustible necessaire. Mais peut-etre que quelque chose de neuf emergera d'ici plusieurs dizaines (centaines?) d'annees.
Exact. Mais cela ne changera pas grand chose quant aux conclusions. Rajoute une poignee d'annees :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for sharing :-) @lemouth I am following. Best of Luck !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is very good @lemouth
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Nice one
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit