Electromagnetism

Electro-Magnetism

Hi steemers, I guess you’ve all been having a good time at steemit, and I hope this article will contribute to one of the great times you’ve all had on this site. let’s go a bit further into natural Science (electro-magnetism…)

The word “electro-magnetism” sounds amazing to me each time I hear it, it’s always like I could do anything with electro-magnetism.
We actually got some electro-magnetic waves like the (RIVUXG)
 Radio waves
 Infarred waves
 Visible spectrum
 Ultraviolet waves
 x-rays, and
 gamma-rays.
The truth is we have got countless others of electro-magnetic waves that cannot be detected with any device yet, a kind of mystery we all have to solve.
Laws guiding electro-magnetism

1. Gauss’s law for electricity,
2. Gauss’s law for magnetism,
3. Ampere’s law with the addition of a new term called the displacement current, and
4. Faraday’s law of electromagnetic induction. With these four equations,

Maxwell predicted that waves should exist in the electromagnetic field.
Equation [1] and [2] implies that all electric and magnetic fields in charge-free space are continuous, that is, the electric fields do not begin or end on any charges. They also show that the electric and magnetic flux do not converge or diverge. Ampere’s law, equation [3], shows that a changing electric field produces a magnetic field, and Faraday’s law, equation [4], says that a changing magnetic field produces an electric field. The fact that a changing electric field with time produces a magnetic field and a changing magnetic field with time produces an electric field, suggests that it should be possible to propagate an electromagnetic wave through empty space
The Production of an Electromagnetic Wave -- An Oscillating Dipole

The electrostatic field of a dipole is reproduced here in figure 29.6[a]. Recall that the electric field E emanates(generates) from the positive point charge and terminates on the negative point charge. This field is an electrostatic field, i.e, one that is constant in time. What happens to this field if the charges consisting the dipole are allowed to vary in position with time?
Figure 29.6[b] shows two pieces of wire connected to an AC source. At the instant shown, one positive charge has moved from the AC source then found at the bottom of the upper wire. As this charge flows from the source, another charge that was initially at the top of the bottom wire has moved into the AC source leaving a negative charge at the top of the bottom wire. At this instant shown, an electric dipole has been created. Just two of the many electric field lines that are present in the space around the dipole are shown in the diagram. After a while, the positive charge has moved to the midpoint of the upper wire, while the equivalent negative charge is found at the midpoint of the lower wire, figure 29.6[c]. The configuration is still that of an electric dipole, but the separation between the charges is increasing with time and the two electric field lines shown in figure 29.6[b] have increased with the increasing separation of the charges, figure 29.6[c]. In figure 29.6[d] the charges have momentarily come to a stop at the ends of the wires. We now show only one electric field line and the electric dipole field line has gotten larger. In figure 29.6[e] the charges have reversed direction and are again midway between the ends of the wire. The beginning and ending points of the electric field are starting to come together. In figure 29.6[f] the charges have almost come together. As the alternating emf of the source goes through zero, the electric field line closes on itself, as shown in figure 29.6[g], since there are no longer any charges for the electric field to begin or end on. In figure 29.6[h] the emf has reversed itself and the positive charge is now at the top of the bottom wire, while the negative charge is at the bottom of the top wire. The direction of the electric field line has become reversed. The same process as in figures 29.6[b] through 29.6[g] continues in figures 29.6[i] through 29.6[m] but with the direction of the electric field line reversed.

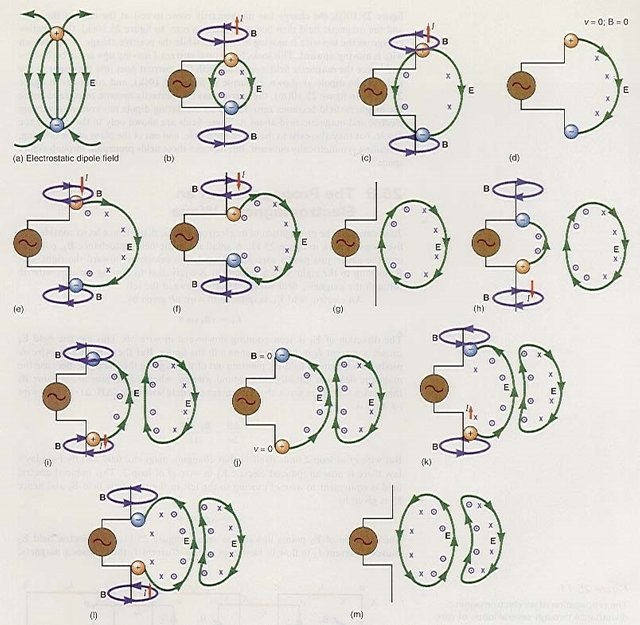
Figure 29.6 The generation of an electromagnetic wave from a dipole.

The examination of figure 29.6 is not yet the entire picture of the radiation. As the positive charge moves upward in the top wire of figure 29.6[b] it represents a current in a wire. The magnetic field is also shown as a purple x in the diagram, standing for the tail of the arrow associated with the magnetic field vector, which is going into the paper. The negative charge moving downward in the bottom wire of figure 29.6[b] is equal(same as) to a positive charge moving upward. Hence, there is also a magnetic field around the bottom wire of figure 29.6[b], as shown. In figure 29.6[c], the magnetic field is in the same direction as in figure 29.6[b]. In figure 29.6[d], however, the charge has momentarily come to rest at the end of the wire. Since the charge is at rest here, there is no current and hence there is no magnetic field around the wire. As the charge on the top wire moves midway down the wire, the current is downward and hence the magnetic field associated with that current now comes out of the paper as shown by the purple circled dot in figure 29.6[e], which stands for the tip of the magnetic field vector. The magnetic field continues to come out of the page in figures 29.6[f] and 29.6[g]. In figure 29.6[h], a negative charge starts to move up the bottom of the top wire while a positive charge starts to move down the top of the bottom wire. A negative charge moving upward looks exactly like a positive charge moving downward. Therefore, the magnetic field associated with this current comes out of the paper on the right side of the dipole, as shown in purple in figure 29.6[h]. The magnetic field continues to come out of the page through figure 29.6[i]. In figure 29.6[j], the charge has momentarily come to rest at the ends of the wire, and the magnetic field then becomes equal to zero. In figure 29.6[k], the negative charge on the top wire is moving downward while the positive charge on the bottom wire is moving upward. This looks like a total current I moving upward in both wires and hence the magnetic field associated with this current goes into the paper at the right of the dipole as shown in purple in figure 29.6[k] and continues in figure 29.6[l]. In figure 29.6[m], the current has momentarily become zero, and hence the magnetic field becomes zero. Hence an oscillating dipole has created a varying electric and magnetic field about it. These fields are shown only to the right of the dipole, but they also exist to the left of the dipole, and out of the plane of the drawing, spreading symmetrically outward. But how can these fields propagate through empty space?
Next time we will talk about the question above.
Stay In touch.
Steemers United.