Hello my name is P-P-Piglet and welcome to my first post on So curious, a b-b-blog where we explore select math & science topics that intrigue the m-m-mind.
The imaginary number √-1 is something that had me stumped for many years. When I was about 12 and first came across it, a wave of bewilderment and fascination crashed through my mind. I had a fair understanding of how to find the square root of a number: find another number whose “square” is the number inside the funny √ symbol. For example, √9 = 3 because 3 x 3 = 9.
Can you find √169? Hint: find a number such that when you multiply it by itself you get 169
But when I tried the same trick with √-1 nothing seemed to work. I dare you to try.
In my head, my math teacher’s voice was droning on about how “a negative times a negative equals a positive” but this conflicted with any attempts I made to preserve the negative sign. Nope, the negative sign would always negate itself into oblivion, to self-combust into the tear-soaked ashes of my despair.
And many years would pass until √-1 would make its way back into my life.
√-1 showed up in my electrical engineering textbook during my freshman year in university. They used the letter j because it is easier to jot down j instead of √-1 (or the letter i works too!). I felt that letting j = √-1 was a bit of a cover up – like shoving some dirty clothes under the carpet. Moreover, they used j in the context of something they called “complex numbers”. Sheesh! Imaginary, complex… who came up with this stuff?
Here are some examples of complex numbers:
1 + j
-5 - 3j
0 + 2j = 2j
0 + 0j = 0
13 + 0j = 13
Remember, j is just shorthand for √-1. In other words: 2j = “2 times the imaginary number”
Also, notice how 0 and 13 are just ordinary numbers. Plain ordinary numbers are also complex numbers! It’s like saying all puppies are dogs. However, not all dogs are puppies (unless you are really imagining things).
The examples above can be represented visually:
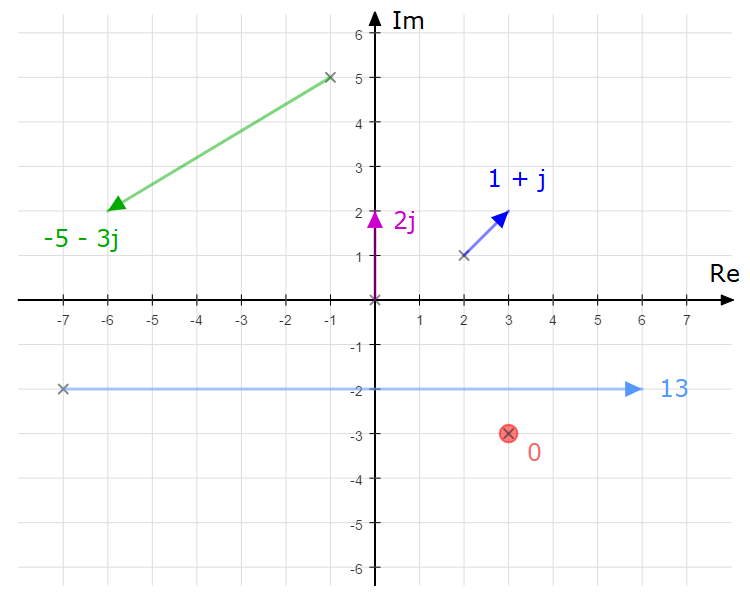
The image was generated using https://www.matheretter.de/formulas/geometry/geodrafter
These arrows (a.k.a. vectors) can be dragged around but their underlying value does not change as long as you respect two rules:
- You don’t change their length
- You don’t change their direction (ok, well 0 doesn’t have a direction… you got me there)
And now we arrive at my breakthrough – a small crack on the shell that contains the mysterious imaginary number. Do you see that little “Im” at the top of the picture? That stands for Imaginary. And the “Re” on the right stands for Real as in real, plain and ordinary… quite boring in fact.
When I first saw this, it stuck with me for several days. But slowly the meaning became clear:
√-1 points into the 2nd dimension
But wait! What is √-1 pointing away from? I mean, we need something that points in the 1st dimension if we are going to have something that points in the 2nd dimension right?
Can you guess what √-1 is running away from?
.
.
.
One Direction! … erm, I mean 1's direction.
So there we have it: taking steps in 1 and √-1 (and their negative counterparts) enables you to walk anywhere on a 2D plane.
Ordinary numbers are 1D: like ants crawling down a clothesline.
Complex numbers are 2D: like ants crawling on your patio table.
To restate my earlier revelation with a little more rigor:
√-1 points in the direction 90-degrees to 1 and vice versa
One way to corroborate this claim is to think about what happens when you multiply an ordinary number by -1. It simply flips the arrow by 180-degrees as in the picture below:
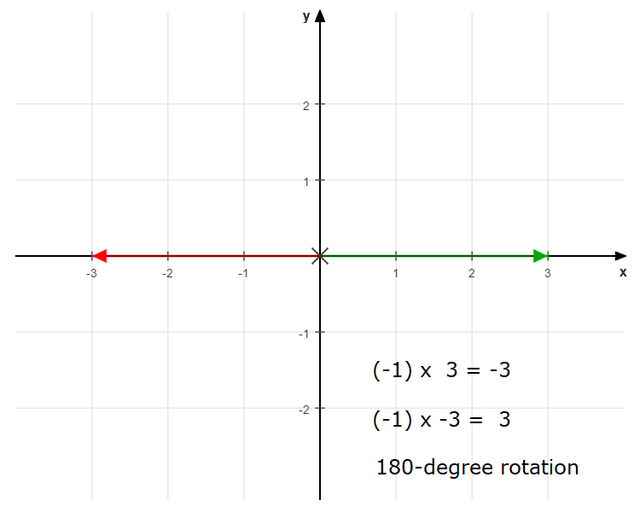.png)
But what if we wanted to rotate by only 90-degrees instead? We multiplied by (-1) to get 180-degrees. What do we need to multiply by to get only 90-degrees?
Whatever it is, let’s call it a Niall.
We know that two 90-degree rotations (getting hit by Niall twice) is the same as a single 180-degree operation.
In other words: (Niall) x (Niall) = -1
So what number exists such that when you square it you get -1?
The imaginary number!
(√-1) x (√-1) = -1
Niall is imaginary, it was all a lie!
To summarize:
Multiplying by √-1 is like rotating by 90-degrees.
Multiplying by -1 is like rotating by 180-degrees.
Multiplying by √-1√-1 is also like rotating by 180-degrees because (√-1) x (√-1) = -1
There are many more interesting facts about √-1 but I do not want my blog to turn into a blob and lose my reader’s attention. Let me know if you think the post was too long or short or just right. Feel free to share anything pertaining to the topic in the comments section below.
Finally, I leave you with a cute, short video related to the imaginary number:
B-b-bye!
haha :-)
just what I was writing about some months ago - cool to see more math people here
https://steemit.com/mathematics/@mcsvi/intuitive-math-everybody-can-understand-complex-numbers-part-1-it-s-all-about-rotation
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hey I just read your post and love your introduction to the complex exponential function. A year ago, I came across this video by 3blue1brown that gives some nice animations to really get a feel for the maths involved. His explanation is a bit too fast towards the end and might require a few replays.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit