Part 2: All About Singularities

第二章: 漫谈奇点

Click here for Part 1: Black holes, thermodynamics and Hawking Radiation
要看第一章: 黑洞，热学定律和霍金辐射请点击这里

Stephen Hawking’s research draws links between the centre of a black hole and the beginning of the universe, from the fact that in both cases, the space time fabric collapses to a point of infinity, and the classical general theory of relativity, and therefore, the nature of spacetime as we know it, breaks down. This point is commonly known as Singularity. In part II of this series, let’s understand what Singularities are, and how Stephen Hawking’s description of this physical anomality lead to an understanding of the origin of the universe.

霍金的研究能把黑洞中心和宇宙起源串连在一起，是因为在这两种情况下时空都会坍塌成一个无限点，广义相对论和时空本身双双被瓦解。这个无限点被称为奇点。在这第二章，让我们尝试理解什么是奇点吧！

Image source

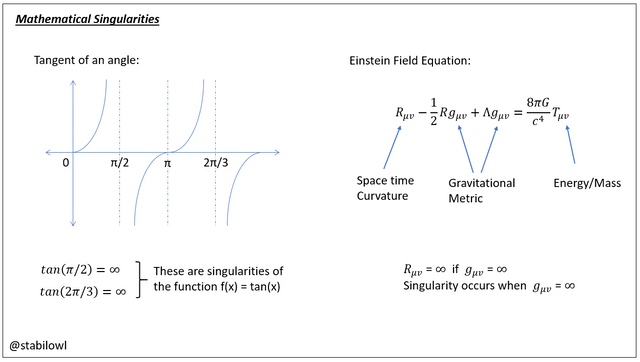
Singularities, in mathematics, in generally where under a certain condition, a value shoots to infinity and become not well defined. A good example is the function tangent. If you try to calculate tangent 90°, you windows calculator will say “Invalid Input”. That’s because tangent 90° is infinity. It blows up to a value that is not well defined. Another good example is division by zero. Gravitational Singularities are conditions that when put into Einstein’s field equation of general relativity, results in infinity in space time curvature. For a condition to be truly a singularity, it must give infinite solutions, no matter what coordinates (reference frame) you use. So a condition that gives infinite solution only under some sets of coordinates are not true singularities. Because of this constrain, for a long time researchers believe that singularities are not physical and is just a mathematical construct.

在数学上，奇点可以理解为一个数学函数变成无限大的点。例如，三角函数里的正切，在角度等于九十度时会变成无限大。那九十度时的正切就是这函数中一个奇点。除数为零也是一个奇点的好例子。那在广义相对论的奇点，就是当爱因斯坦引力场公式的解变成无限时，时空就为出现奇点。因为广义相对论的运算可以用不同的坐标，而一个真正的奇点要在所有的坐标的运算下的都是无限，所以在霍金前很多物理学家都认为奇点是不存在的。

singularities

This changed when Stephen Hawking, during his PhD, argued that singularities are inevitable. In his thesis “Properties of expanding universes”, He based his argument on work done by Roger Penrose earlier, who treat singularities as “Incomplete Geodesics” in the space time fabric. Geodesics are lines on a curved surface that is the shortest path between two points. For example, the shortest route between the city of New York and Hong Kong is a curve passing through north pole. This is the geodesic between the two cities. The curvature in the space-time fabric also has a corresponding geodesic between two points.

然而霍金在他的博士论文中推翻了这假设，证明了奇点是存在的。在他的论文论澎涨宇宙的属性里，他用了物理学彭罗斯的观点，把奇点理解为时空结构里的不完整的测地线。测地线是几何学里的概念，是一个曲面上两点的最短线。以地球为例，一辆飞机从香港飞往纽约会往北极飞，是因为这大曲线才是这两个城市的最短的距离，是它们的测地线，而不是地图上的直线。

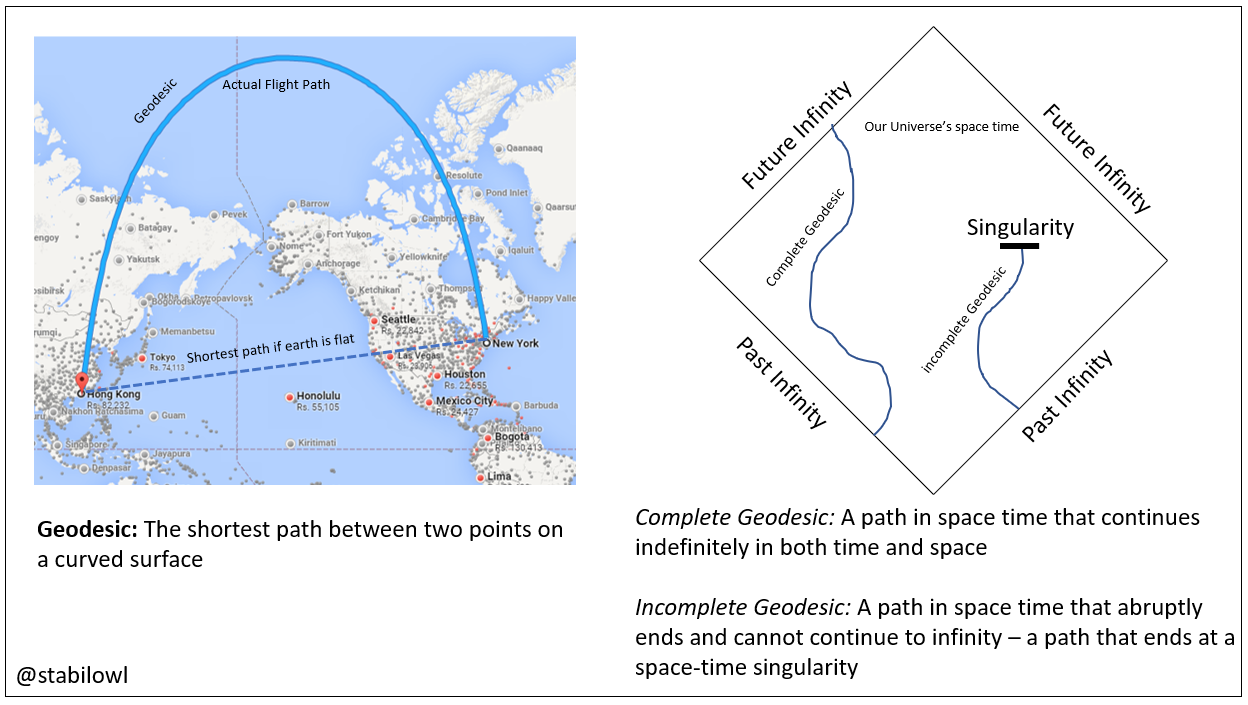
geodesics
Flight map image source
Diagram adapted from Stephen Hawking’s “The Nature of Space and Time”

It can be generalised to simply a line drawn on the space-time fabric. Usually this geodesic just continues on indefinitely on the spacetime fabric: someone who travels along this geodesic can continue to do so indefinitely. This is known as a complete geodesic. However, there are cases where the geodesic would abruptly stop. This is known as an incomplete geodesic in spacetime, and Penrose recognises that this is essentially a singularity. And Hawking in his thesis uses geometrical properties of the spacetime geodesic to show that a spacetime what does not have singularity would lead to contradicting statements, thereby proving mathematically that singularity exists in our universe.

在时空结构里的测地线就是时空中的轨迹。通常这轨迹是在时间和空间都是无限伸展的，一个观察者可以沿着这轨迹一直走下去。这样的轨迹是完整的。然而有些轨迹可能走到一半就突然中断，时间和空间在这轨迹上突然终止。这不完整测地线中断的点就是时空奇点。霍金就是用了这几何学的概念，用几何属性论证一个没有不完整测地线的宇宙是自相矛盾的，从而反证了宇宙中奇点的存在。

A part of Stephen Hawking’s Proof. From his thesis “Properties of expanding universes”

After his PhD, Stephen Hawking continued to work on the topic of singularity. Together with Rogen Penrose, they formulated the Penrose-Hawking Singularity theorem, which are a general set of theorems which consider how different universes under different conditions (essentially different geometric constructions of a universe in the framework of the general relativity) can result in the formation of singularities. In Hawking and Penrose’s “The Nature of Space and Time”, Hawking generalised that singularity theorems contain three different conditions or constrains: An energy condition, a global structure condition, and a gravitationally trapped region. An energy condition can be weak (where energy density in the space-time is greater than zero), strong (where the energy density in the space-time is much greater in order to make all gravitational effect for all time-like vectors positive), or generic (where strong energy condition holds and that every time-like or space-like lines could encounter somewhere gravitational lensing.); the condition on global structure specifies special conditions that the space-time geometry was satisfied; and for the third condition, a trap region is a region in space time where both outgoing and incoming rays into the region converges.

博士毕业后，霍金继续和彭罗斯合作研究奇点。他们研究出彭罗斯-霍金奇点定律，为不同宇宙中奇点存在所需的条件定下了限制。在时空的本质中，霍金描述的一般奇点定律所需要的三个要求: 能量要求，综合结构限制和引力阱区的存在。能量要求就是一个宇宙的总能量值需要达到的水平。弱能量要求下，只要宇宙总能量大于零就可以了。强能量要求下，宇宙总能量要大于所有时间矢之间引力大于零所需能量。而广能量要求则需要宇宙总能量大于强能量要求并可在宇宙里引起引力透镜效应。综合结构限制是对宇宙的时空结构所设的限制。而引力阱区则是时空里光线进入和离开都被引力限制而汇集。

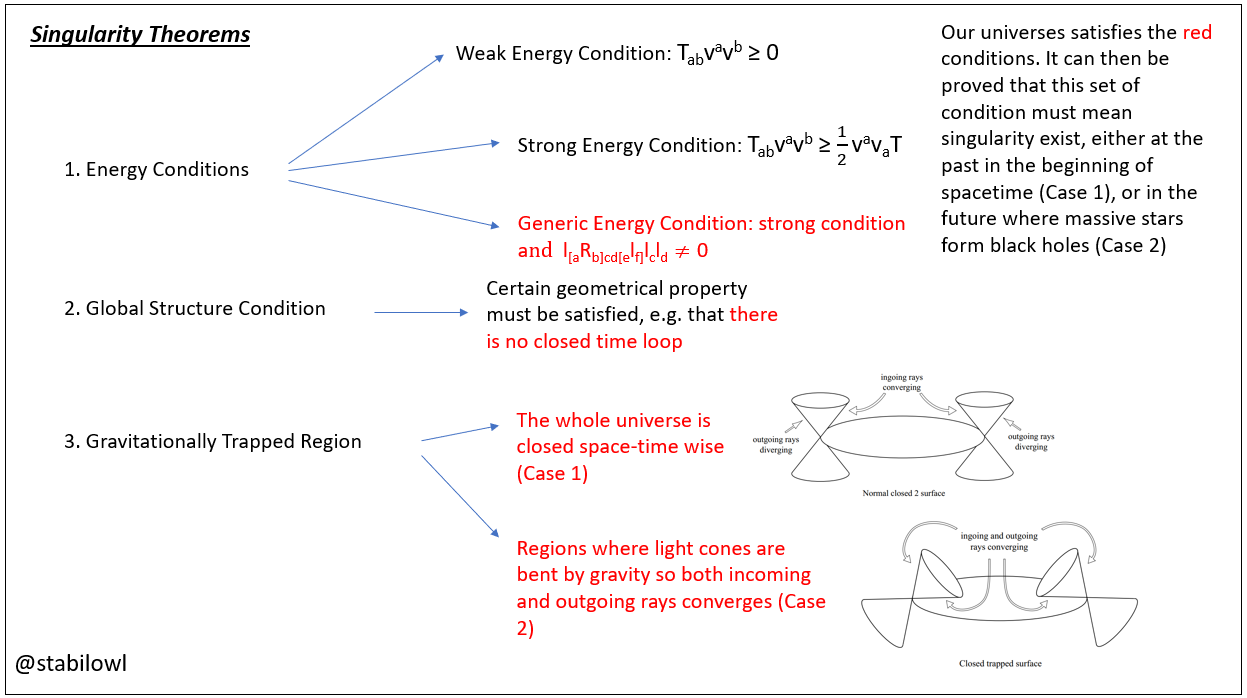
singularity theorem

Adapted from “The Nature of Space and Time”

The strength of these constrain can be varied in the expense of one another. For example, if the energy condition is weak, then more constrain must be applied to the global structure and/or the geometry of the trap region in order for singularity to occur. They then went on and show that under the generic energy condition, which although strong but is achieved in our current universe, the condition on global structure can be relaxed to a simple constrain of no closed time loops (i.e. time does not go backwards), which is also satisfied by our universe, to guarantee a singularity. Furthermore, the theorem shows that there are two possible ways this singularity can occur for a particular path on our space-time: either in the future at points where gravitational collapse occurs due to high concentration of energy/mass – blackholes - and these are end-points in the incomplete geodesics. The other possibility is at the starting point of all geodesics on the space-time fabric in the past – the beginning of the universe as we know it was a singularity. This reinforced the idea that the universe comes from a big bang, and is one of the most important discoveries in modern cosmology.

这三个限制或要求是互补的。例如若果一个宇宙只满足弱能量要求，那么时空结构上的限制要变多增强才能保证奇点的存在。而彭罗斯-霍金奇点论正好相反，他们用了最强但我们所在宇宙仍然能满足的广能量要求，从而把结构限制减少到只有一条我们所在宇宙也能满足的条件: 时间不能循环，而得出了两种形状引力阱区所引发的奇点都会存在: 在时间未来超大质量而形成的奇点(黑洞），和在时间过去所有测地线的起点（宇宙诞生时）的奇点。就是说他们证明了宇宙起源于一个奇点，宇宙诞生于一个奇点的大爆炸。

As the Penrose-Hawking Theorem shows that singularity does exist in our universe, it leads to the question of what happens at these singularities. As pointed out by Hawking, the existence of these singularities inherently means that the general theory relativity breaks down at these points and therefore, it is not a complete theory as it failed to describe the behaviour of gravity at these points. While this is especially true for the singularity in the past, i.e. the big bang, Penrose, comes up with a proposal call Cosmic Censorship for singularity occurring in the space-time future, which says that naked singularities, where singularities are directly accessible to observers, does not exist in nature. This means that in the observable universe, Physics still works (as the singularities are not observable)

Two formal description of the Cosmic Censorship is further developed by Penrose, Hawking and Nobel Laureate Kip Thorne. The Weak Cosmic Censorship formulation states that apart from the Big Bang, all singularities occured within the event horizon, a path in the spacetime around the singularity which enclose a region of spacetime that is not in the past or future of our space time. This of course, is a blackhole, as light or information within this region of spacetime cannot escape to infinity. A consequence of the weak cosmic censorship is that event horizons and singularities cannot intersect each other in spacetime. It follows that the size of the event horizon can never decrease with time, otherwise the spacetime lines that generates the event horizon will intersect, which is geometrically not allowed. Similarly, as the event horizons of two blackholes cannot be converging in spacetime, when two blackholes collide the resulting blackhole can only be bigger not smaller. This is, of course, the second law of blackhole mechanics.

霍金指出这些奇点的存在引证着经典场论和广义相对论的漏洞，因为奇点里的物理是不能用相对论解释。然而，彭罗斯还是想尝试经典场论解决这问题。他臆造了宇宙审查假说，认为大自然里没有暴露的奇点。他和霍金和诺贝尔奖得主基普.索恩制定了弱形式和强形式审查假说。在弱形式假说里，除了宇宙起源的奇点外，所有奇点都被包围在一个不是任意其他时空的过去和未来的时空中。这个时空就是黑洞，而这时空的边界就是事件视界。在视界外的引力作用完全可以用经典场论来解决，而在视界内的是黑洞的一部分，所以可以用经典黑洞力学来解决。弱形式假说的一个属性就是不同奇点的事界是不能汇集的。这就是说黑洞相撞时事界面积只能变大，也就是上一章所说的黑洞第二定律。

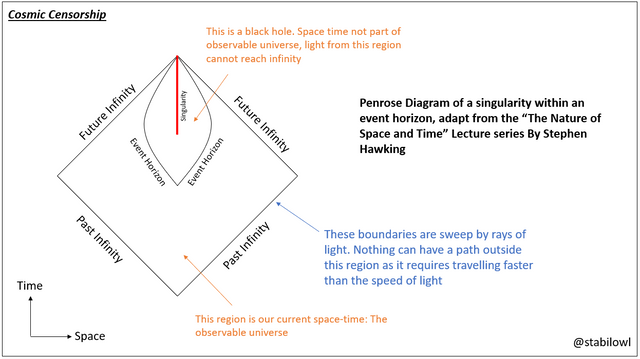
cosmic censorship
Adapted from “The Nature of Space and Time”

A strong cosmic censorship is also developed, which states that General Relativity is a classical theory, and that the fate of all observers is measurable and predictable given an initial condition. The only way this can happen is if singularities are concealed in black holes, and the fate of an observer approaching the singularity is predicted through the general relativity description of black holes.

An interesting story about the Cosmic Censorship is that Kip Throne who although co-developed the formulation, bet against the cosmic censorship being true with Stephen Hawking. It turns out that there are situations where, at least in computer simulations, that naked singularities could exist. The strong cosmic censorship also implies a completely classical picture of gravity, which is widely accepted to be not adequate enough to explain many phenomena associated with black holes and the beginning of the universe. So although Stephen Hawking still held onto the bet until he died by putting additional conditions to the occurrence of naked singularities, he had also spent a major part of his life searching for solutions to explain the physics at a singularity through quantum gravity. In the next post, I will be visiting some of the solutions to quantum gravity that he proposed, as well as the impact of his work on the famous string theory, which is currently the most promising theory that unites general relativity and quantum mechanics.

在强形式的审查假说里，广义相对论是个绝对的经典理论，所有宇宙中的观察者的时空轨迹都能准确的预测。只有在所有奇点都被经典的黑洞包围下，强形式假说才能成立。有趣的是索恩本人也不相信审查假说，并跟霍金打赌假说不成立。虽然霍金生前对这场打赌还没有认输，他也知道只有把量子力学和广义相对论二合为一才能真正解决奇点这个问题。在下一章，让我们探讨一下霍金对量子引力的解释，和霍金的研究对其他的万物论，例如弦论的发展的贡献。

References:
http://vrs.amsi.org.au/geodesic-incompleteness-spacetime/
https://en.wikipedia.org/wiki/Einstein_field_equations
https://en.wikipedia.org/wiki/Gravitational_singularity
https://en.wikipedia.org/wiki/Stephen_Hawking
https://en.wikipedia.org/wiki/Penrose%E2%80%93Hawking_singularity_theorems
Hawking, S. (1966). Properties of expanding universes (doctoral thesis)
Hawking, Stephen; Penrose, Roger (1996). The Nature of Space and Time. Princeton University Press. p. vii. ISBN 9780691145709