Is there a difference between centripetal acceleration and centripetal force, and if so, what is it? If we know the mass of an object moving along a curved path, how can we calculate the centripetal acceleration and/or force?
Suppose we have an object with a mass of 10kg, which is fixed to a rotating shaft by a rope 10m in length. The shaft is rotating at 60rpm. What is the centripetal force?
First, we need to know how centripetal force is calculated. Like any other force, it is equal to mass (m) multiplied by acceleration (a)
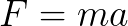
We know the mass of the object; however, we do not know the acceleration. Not to fear, physics and math come to the rescue with the following equation to find acceleration
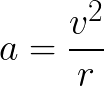
This tells us that acceleration (a) is equal to the square of an object's tangential velocity (v) multiplied by the radius (r) of the arc through which it is moving. An important note to remember is this equation is for centripetal acceleration, and not other forms of acceleration.
Very well, we know the radius of the arc through which our object is moving, but we still do not have all the pieces of the puzzle. We still need to find the tangential velocity of the object, and again physics and math save us with the following equation
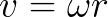
We see from this equation that tangential velocity (v) is equal to an object's angular velocity (w) multiplied by the radius of the arc through which it moves. Another important note is that angular velocity is expressed in radians per unit of time, and so we must first convert our 60rpm to radians-per-time unit
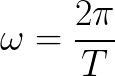
This equation states that angular velocity is equal to 2 pi divided by time (T). Although our time unit is expressed in minutes, our angular velocity should be expressed in seconds for our overall problem, so we will first convert 60rpm into second-based units, then use the above equation to convert the result to rad/s
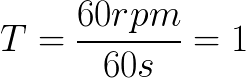
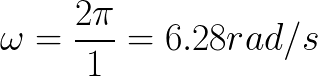
We now see our object has an angular velocity of about 6.28 radians per second, which is equal to one revolution per second, or 60rpm. With this information we can now calculate our object's tangential velocity
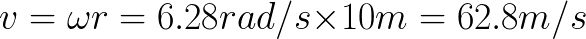
Our object has a tangential velocity of 62.8 meters per second, and so the the centripetal acceleration is
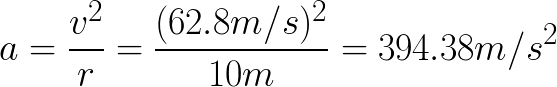
Finally, we have reached a point where we can use our centripetal acceleration of 394 meters per second per second (meters per second squared) to calculate centripetal force
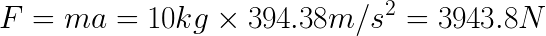
This means that the rope securing our object to the rotating shaft must be able to withstand at least 3943 Newtons, otherwise it will break and the object will go flying off. To put this in perspective, 3943N is about equal to a stationary mass of 402kg (or 884lb) hanging on the end of rope.