THE UNIVERSE AS AN IDEAL OSCILLATING SYSTEM

        Decades of experiment have resulted in the consensus that the visible matter in the universe was at one time collated in an area of extreme density, and that this dense region exploded outwards to form the present state of the visible universe. From this initial assumption it will be shown that space itself must be imbued with density and pressure, that the behavior of the local universe approximates an ideal oscillating system, and that the energy of this ideal system can be modeled by Euler’s equation:

e^ix= cos(x) + isin(x)

        The universe may very well be infinite, but for the sake of the following thought experiment we will refer only to the “local universe,” which we will treat as a closed system. While we cannot say with certainty that all the visible matter in the local universe was once condensed at a single point, we know that at one time the matter was far more condensed than it is now. Thus, we can use the concept of the singular, ultra dense point as an ideal limit. At this hypothetical moment of singularity, the average kinetic energy of the local universe would be zero, because the net relative motion of all visible matter would be zero. Meanwhile, there would have to be a maximum amount of potential energy to compensate for the lack of kinetic energy and satisfy the law of conservation of energy. This maximum in potential energy would be physically embodied by the immense outward pressure resulting from the superposition of all visible matter. Instantaneously, this pressure must begin to force the condensed matter outward, and in doing so transform itself into kinetic energy. In accordance with the law of conservation of energy, the potential energy must decrease by the same rate at which the kinetic energy increases. The expansion of the system continuously accelerates so long as there remains positive potential energy, in the form of pressure, to exert outward force upon the visible matter.
        At this point it is inconsequential whether we refer to the unseen pressure as a consequence of "dark matter" or of the space itself-- the only thing we can know with certainty is that energy must be expended in order to generate the outward force. Thus, eventually, the positive potential energy must be depleted, the velocity and kinetic energy of visible matter must simultaneously reach their maximum, and the outward acceleration of visible matter must cease.
        Throughout this multi-billion year transformation, a negative potential energy has existed in the form of gravitational attraction between disparate matter. Until this point, we have been justified in calling the universal potential energy positive, because the outward pressure vastly exceeded the inward force of gravity. Now that the outward pressure has expended itself, the scale is tipped in favor of the negative potential, which will continue to grow in magnitude and cause the visible matter to decelerate in its outward expansion.
        In our discussion of the positive potential energy, I stated that the physical mechanism of the outward pressure was inconsequential to our model-- regardless of the form of this pressure, it will behave according to the same rules that govern all other forms of pressure. We run into a brief stumbling block when we consider the nature of the negative potential energy. Gravitational force, in the classical Newtonian conception, is said to decrease with the square of the distance between two masses. If we rely on this conception in our model, the negative potential would approach zero as momentum carried matter further and further away, because the added distance would proportionately sap the attractive force. A contradiction would arise, because the potential and kinetic energy of the system would both decrease in magnitude simultaneously. The sum of the two magnitudes must remain constant to satisfy the law of conservation of energy. Energy will only be conserved if the attractive force grows stronger as matter coasts further outward, in the same manner of a spring stretched further and further past its equilibrium point.
        We have referred to the positive potential energy as an outward pressure, which would imply that it is a function of energy density. It stands to reason that the negative potential energy must take the form of a negative pressure-- an inverse function of the same energy density. Once the site of the initial outburst has expended its energy, the interior becomes less dense than the exterior. A roughly analogous situation would be the underwater explosion of a stick of dynamite; water and the matter of the dynamite itself are thrust outwards by the initial release of pressure. For a brief interval, a sphere of low pressure is created around the origin of the explosion, a result of the surrounding water having been pushed violently outwards. Inevitably, water must rush back toward the origin to fill this relative vacuum, carrying with it bits of dynamite that are analogous to the visible matter in the universe.
        To resolve the energy conservation paradox, we must allow that space itself has a density and pressure like the water in the dynamite analogy, creating a flux which can affect the motion of visible matter.
        Armed with this new understanding of gravity, we can now finish modeling the evolution of our local universe. The average of the universal potential energy has now tipped onto the negative side of the scale, gradually diminishing the kinetic energy and decelerating matter as it continues its outward motion. The further outward the matter coasts, the greater the region of low pressure and thus the greater the negative potential energy, increasing the deceleration of the projected matter until the matter finally comes to a halt.
        At this moment, the potential energy will have reached its negative maximum, and the average kinetic energy will once again be zero before tipping into the negative as the matter begins to be pulled backward into the region of low density. As the matter accelerates back to the center, increasing the negative kinetic energy, the region of low pressure accumulates density and the total potential energy gradually shifts in the positive direction. Kinetic energy and the velocity of matter will reach a negative maximum at the moment that potential energy becomes neutral, at which point the growing density of the inner space will begin to decelerate the accumulation of matter. The kinetic energy and velocity of matter will decrease as the potential energy becomes increasingly positive, and ultimately they will reach zero at the moment that potential energy once again reaches its positive maximum and matter is condensed to a singularity.
        Having come full circle, so to speak, the cycle must repeat. A new explosion commences, and matter is flung outwards yet again, destined to repeat this eternal oscillation. Having described an entire cycle, it is now clear that our potential energy graph is a cosine wave and our kinetic energy graph is a sine wave.
        The astute reader will undoubtedly have already noted that the sum of a sine and cosine wave is not a consistent value, and thus it would seem that energy is not conserved after all. This problem is a result of placing both graphs on the same axis. Since they are a measure of two different things, we have no basis to put them on the same axis. If we place kinetic energy on its own axis, the z axis, then the problem is resolved. The sum of the two energy vectors at any x (time) value will always have a magnitude of one and thus the total energy will remain constant at all moments in time, in accordance with the law of conservation of energy.
        Conveniently, the graph as we are now describing it is identical to the graph of Euler’s equation: e^ix= cos(x) + isin(x)

[ABOVE: Universal oscillation depicted from big bang (left), to big crunch (middle), to the next big bang (right). Potential energy in green, kinetic energy in purple. X values in radians, where the middle is pi and the far right is 2pi. This PE/KE graph can just as easily be applied to ideal springs, pendulums, or any other ideal oscillating system.]

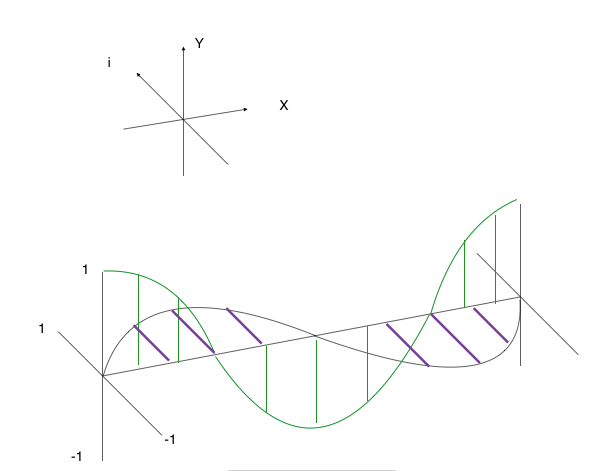
        Multiplication by the imaginary unit i has the effect of rotating a number 90 degrees into the i dimension. By multiplying our sine graph by i, we are merely saying that its values will exist on the imaginary axis instead of the real (y) axis.
        Euler’s equation (often presented in the form of Euler’s identity: e^iπ =-1) is famous in mathematics because it relates imaginary numbers, the natural logarithm, trigonometry, as well as the ratio of a circle’s diameter and circumference, all in a single equation. It is a magnificent coincidence that, as we have shown, this equation also describes the potential and kinetic energy of an ideal oscillating system. Pythagoras, who proposed that the universe was made entirely of number, would probably feel vindicated to learn that one of the most crucial statements in mathematics may also describe a physical law.
        It is doubly rewarding to consider that the very universe we inhabit may approximate this ideal oscillating system; though there is still a variable that we cannot completely account for: the size of space itself. While all the matter we can see was once packed together far more densely than it is today, we cannot reasonably declare that this is all the matter in the universe. The universe might just as easily be infinite, and our “big bang” merely a small pop in an infinite sea. The infinitude of space would also mean that the local universe cannot approximate an ideal oscillating system. An ideal oscillating system can have no energy loss, but if our visible universe is only a small part of an infinite space, it is inevitable that our local system would spill energy out into the surrounding regions, continuously losing energy until the system ceases to oscillate.
        While our universe may not be a perfect oscillating system, the thought experiment has justified itself by modifying the traditional notions of space and gravity. The law of conservation of energy demands that space itself be imbued with energy. In the classical conception which regards space as vacuum, the local universe would deplete its kinetic and potential energy simultaneously, resulting in an overall diminishment of energy.

Cover Photo: Image Source