Geometrical demostration of the product (a + b)(a - b)

Hello Friends of steemit, this time I'm bring You another demostration of an important an useful algebra formula that we use in cases of factorization. The demostration will make using geometry like the demostration of notable product previously published.

Let get start considerating two squares, one having sides labeled with the letter a and area equal to a^2 and the other square having sides labeled with letter b and area equal to b^2 (Fiure 1)

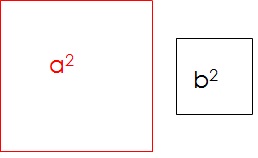
Figure 1

Now we will take the square b^2 and will put inside the square a^2 (Figure 2)

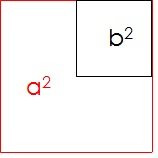
Figure 2

Next, we draw a line starting in the lower left corner of square b^2. Notice that, the pointed line (Figure 3) has a length equal to the difference between the sidaes a and b, I mean, a - b. So, with this line we will have a rectangle, labbeled with capital letter C (we use lower cast letter to label sides) and having sides (a - b) and b.

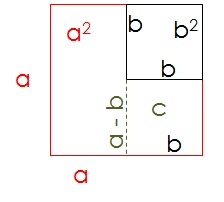
Figure 3

We can see, from Figure 1, a difference between the squares as is shown in the Fiure 4, the part pinted with light blue is equal to that difference: a^2 - b^2, and also we can note that the area of the rectangle C is included into the area a^2 - b^2

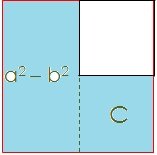
Figure 4

Now, if we cut the rectangle C and after we will put over the square a^2 as we can see in Figure 5, we have a new rectangle with sides (a + b) and (a - b).

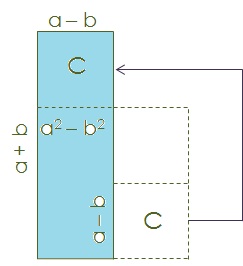
Figure 5

And the area of this new rectangle we can calculate by multiplying the sides (a + b) x (a - b), but this area is equal to a^2 - b^2 that is pinted again with light blue.
So in this way we have proven that: (a + b) x (a - b) = a^2 - b^2.

Once again we can obtain an algebra formula Through geometry, my point is the same of the last publication: all mathematics is constructed by geometry.

Refference: Algebra of Aurelio Bldor.

@steemstem