Vi siete mai domandati come si ottiene il seed phrase?
Il Seed phrase è una serie di parole che permettono di generare o rigenerare l'albero delle chiavi, di derivare quindi il wallet deterministico.
Quindi se qualcuno trova il seed phrase, va da se che ha a disposizione tutte le nostre chiave e di conseguenza i nostri bitcoin.
Quindi conservatelo in un posto sicuro !
Il BIP39 definisce la creazione del mnemonic code e del seed.
mnemonic code, mnemonic phrase, mnemonic recovery phrase, mnemonic seed, seed phrase. Sono tutti sinonimi :)
La sequenza di queste parole sono sufficienti per ricreare il seed, e da qui ricreare il wallet HD e le chiavi derivate.
Seed Phrase -> Seed-> Chiavi Master -> Chiavi
Se si usa lo standard mnemonic, abbiamo a disposizione un dizionario di 2048 parole, con 2048¹² combinazioni.
Tali parole sono selezionate con cura per non essere simili tra loro e non sbagliare a scriverle.
Gli steps da seguire
- Partiamo da 128 bits, 32 caratteri esadecimali, che rappresentano l'entropia.
- Applichiamo lo SHA256 e appendiamo i primi 4 bits (cioè 1 carattere esadecimale) in fondo all'entropia.
- Questo rappresenta il checksum.
- Convertiamo il risultato ottenuto in base2.
- Il risultato binario viene diviso in 12 segmenti da 11 bits ciascuno, ogni segmento rappresenta una parola.
- È necessario convertire il valore delle singole caselle in base10, in modo tale da ottenere un numero che si può mappare nel dizionario.
- Prendiamo i valori corrispondenti dei bits accesi, cioè dove è presente il numero 1, e gli sommiamo.
- Il risultato che otteniamo è un numero, che mappato al dizionario inglese dato dalle 2048 parole, da come risultato accident.

Start!
Partiamo dall'entropia 0168071cf29dbdf232de82fa34acb933
applichiamo quindi lo SHA256 e prendiamo il primo carattere del digest.
printf 0168071cf29dbdf232de82fa34acb933 | xxd -r -p | sha256sum -b | head -c 1
3
Il 3 è il checksum che dobbiamo appendere all'entropia, e poi convertire in base2.
echo "ibase=16; obase=2; $(echo 0168071cf29dbdf232de82fa34acb9333 | tr '[:lower:]' '[:upper:]') " | bc| tr -d '\n'
risultato:
10110100000000111000111001111001010011101101111011111001000110010110111101000001011111010001101001010110010111001001100110011
Ottenendo così codice binario da "incasellare".
printf 10110100000000111000111001111001010011101101111011111001000110010110111101000001011111010001101001010110010111001001100110011 | sed 's/.\{11\}/& /g'| tr " " "\n"
10110100000
00011100011
10011110010
10011101101
11101111100
10001100101
10111101000
00101111101
00011010010
10110010111
00100110011
0011
Come vediamo non abbiamo delle caselle da 11 bits ciascuna, per renderle omogenee dobbiamo aggiungere 7 bits di zeri all'inizio
printf 000000010110100000000111000111001111001010011101101111011111001000110010110111101000001011111010001101001010110010111001001100110011 | sed 's/.\{11\}/& /g'| tr " " "\n"
00000001011
01000000001
11000111001
11100101001
11011011110
11111001000
11001011011
11010000010
11111010001
10100101011
00101110010
01100110011
Convertendo il primo risultato in base10
echo "ibase=2; 00000001011" | bc
Otteniamo il risultato 11
Possiamo nel dizionario https://github.com/bitcoin/bips/blob/master/bip-0039/english.txt che parole è mappata all'indice 11.
La parola che troviamo è accident.
Attenzione, la lista parte da 1, quindi l'elemento è n+1.
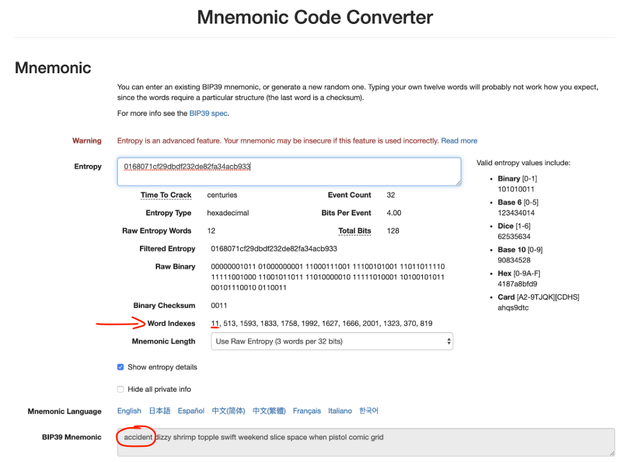
Abbiamo la possibilità di verificare il nostro risultato utilizzando il sito https://iancoleman.io/bip39/ ed inserire l'entropia che abbiamo utilizzato
--
Se vuoi approfondire l'argomento, guarda questo corso completamente in italiano 🚀
Se invece vuoi offrirmi una birra 3CEraggS51ePmB9KSVcXWSPWtdrXPNY91B 🍺
--