
I am a Computer Science graduate but haven't been in touch with the field for the last ten years. At times, I think of getting back to it but the very thought overwhelms me. This lesson was a reminder that basics never change and it's probably time for me to roll up my sleeves and bite the bullet. Thank you @ sergeyk for this interesting lesson which proved to be a great motivational factor behind this post.
Programming Language : C
Online Compiler : Programiz
Task # 1
Come up with your own example similar to float f=7/2;the one that illustrates the loss (distortion) of value when dividing. But show how to fix it. Explain why this happens and how you fixed it?
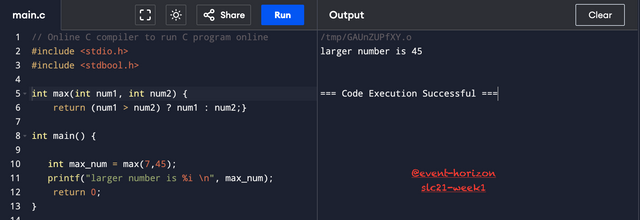
Division seems like one of the simplest arithmetic operations. But, is it? Computers seem to know everything. But, do they? Let's find out. I will write a simple code for division in C.
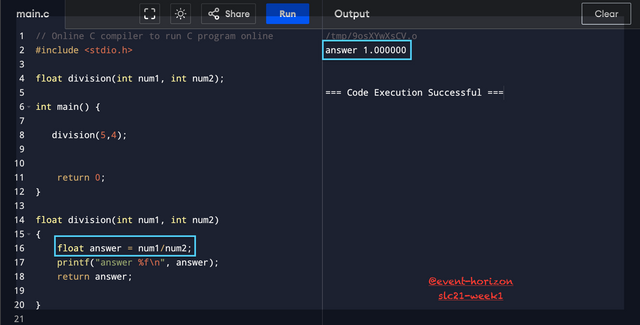
I have used float data type because the answer of 5 divided by 4 won't be a whole number or an int but a decimal number with fractional part. But if you see the answer on the right panel, it says 1.000000. There is a fractional part but it's not right. You can try giving it different inputs, but if the answer is not a complete whole number, then it will always lose the fraction.
Let's make some changes to the code.
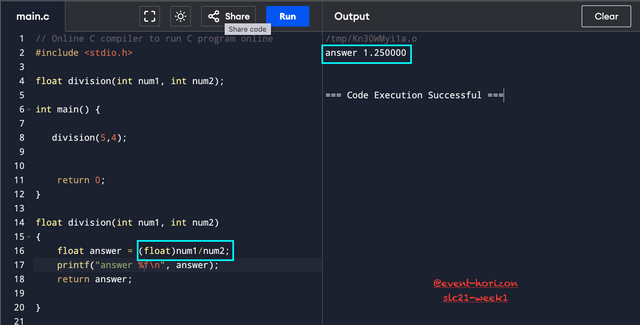
Now we got the correct answer 1.250000. I cast (forced-typed) one of the input numbers num1 to float which was an intduring the computation. We needed to perform a floating arithmetic operation which means at least one of the operands should be a floating number. What we were doing in the previous code was integer-arithmetic operation and assigning the result to a variable of float data type.
Another way is to take float directly as input but this should mainly depend on the scope of the program.
Task # 2
Choose the type of data yourself and illustrate the limitation of its range: demonstrate the limit - from below (transition through the minimum value) and from above (transition through the maximum value. Also, demonstrate the transition through the limit during the multiplication operation, and explain the results.
In the real world, we talk numbers in a decimal system, but computers do it in binary. Every number, letter, and character has a binary representation. Each digit in a binary number is called a bit and 8 bits make up one byte. In programming, there are different data types which define which kind of data a variable can hold and range of that data depends on bit-length. A character (data type char) is stored in one byte. An integer is stored in 2 or 4 bytes. A float is stored in 4 bytes. A double is stored in 8 bytes. To put it simply, a character cannot have 9 bits or an integer cannot have 8 bytes.
I will demonstrate the limitation of one of the most commonly used data type int through the following code.
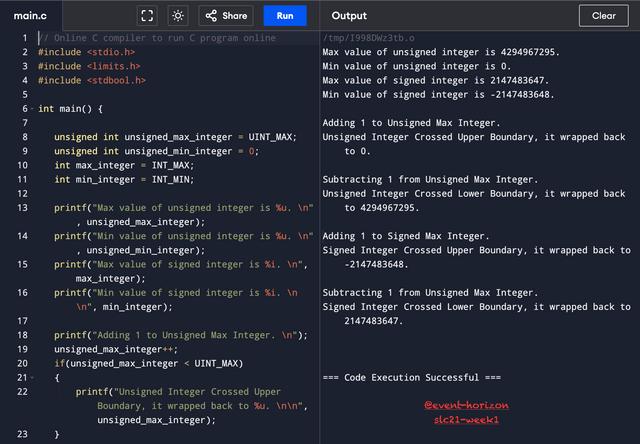
In this code, I have printed out the max and min values of signed and unsigned integers using built-in functions from the limits library and then I have pushed the limits of those extreme values by adding and subtracting from them.
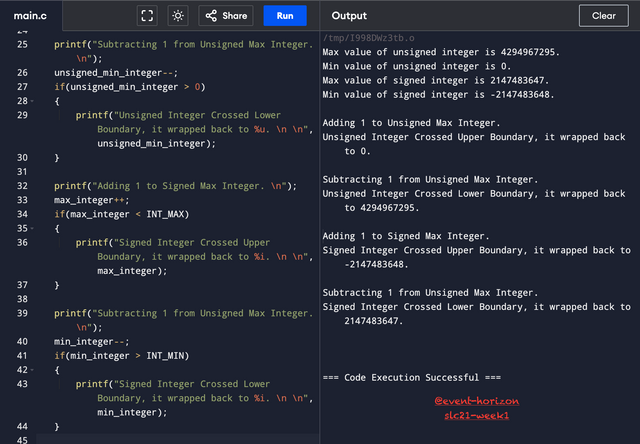
It can be seen that after doing an increment in max values, the new number doesn't become greater than the max value, but it rounds back to the smallest value. Similarly, by doing a decrement in the minimum values, the new number doesn't become smaller than the minimum value, but it rounds back to the maximum value. Languages are usually designed to wrap the values and keep them within their specified range to avoid overflow and underflow.
Like already said, an integer cannot have more than 32 bits. Adding to maximum unsigned int would try to push to 33 bits. Subtracting from minimum unsigned int should give a negative number but unsigned numbers can't be negative. Adding or subtracting to the maximum or minimum signed ints wouldn't change the bit length but it will tamper with the sign bit, as a result affecting the overall value.
Multiplication Overflow in Integers
I have created two functions (both for signed and unsigned integers) to check overflow in multiplication. Both return a bool value, true if overflown and false if not. I have tested the function by giving different kinds of inputs.
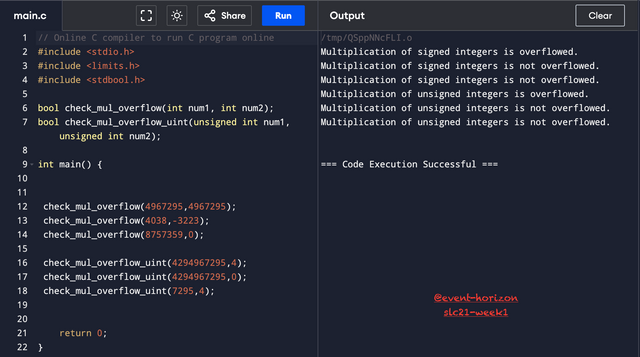
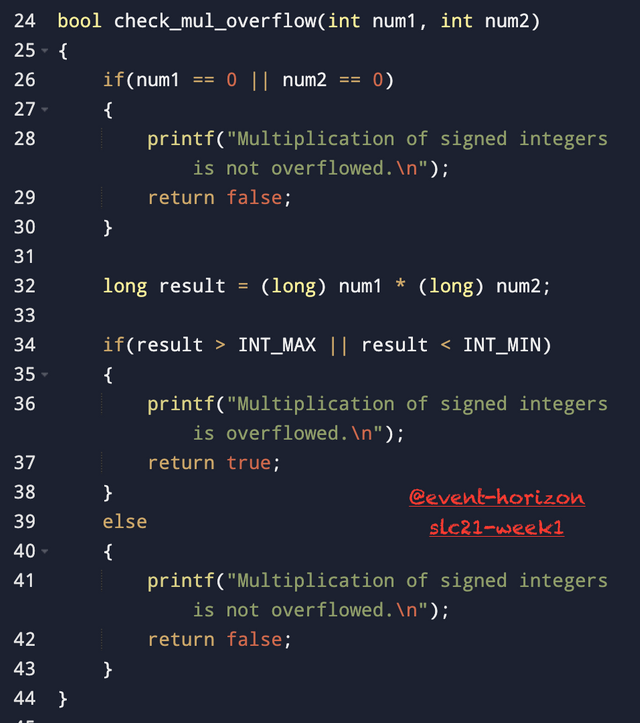
To check the signed integers, I have typecast the inputs to long and stored the result in a variable of long type. Because it can store much larger values. Then I simply checked if the result was bigger than the max value of the signed int or smaller than the min value of the signed int; if that is the case, that means the result doesn't fall in the range and is overflown.
 | 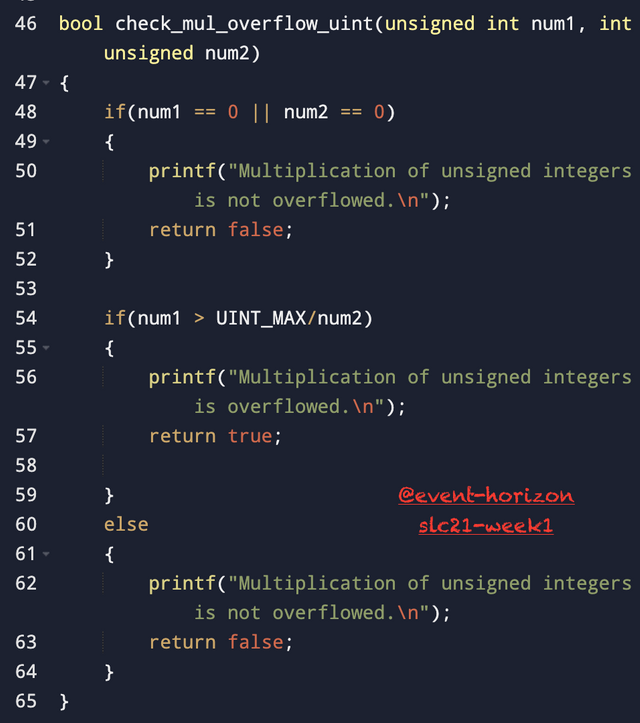 |
As for unsigned integers, I went with this logic that if num1 * num2 is less than the maximum value, then mathematically num1 should be less than maximum_value/num2. But if that's not the case, then that means multiplying both numbers would yield a bigger number than the maximum value, causing an overflow.
The latter is simpler logic, but it can't be applied to negative numbers; that's why I had to typecast in the former case.
Task # 3
Find your own example of 0.1!=0.1, meaning there is a certain value in a variable, but the check shows a different number. Or 0.1+0.2!=0.3. Why is this happening?
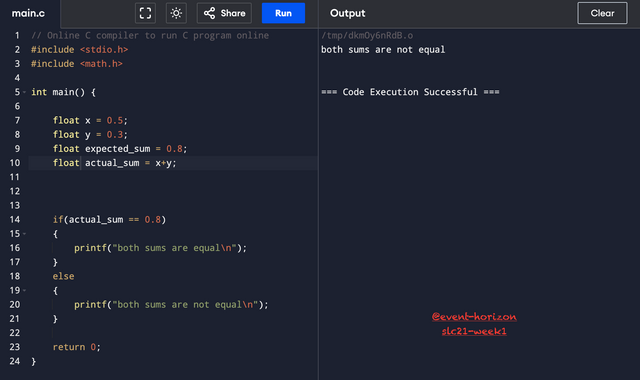
In binary representation, real numbers can be tricky. In the following code, you can see that 0.8 != 0.8, or perhaps the actual sum is different from the expected sum, which is 0.8. While handling floating point numbers, precision is important. In the example, the actual sum might be slightly different. But the difference is so small that we ignore it in the usual decimal system.
If I change the data type from float to double in this example, the computer will say the sum is equal. It's because in float, the data is valid upto 6 decimal places; the rest is invalid. But for double, it is 15 valid places, and a little more for long.
If, for some reason, we can't use the higher-ranged data type or we are dealing with infinite decimal places, then we use epsilon. It's a very small positive value, which if greater than the difference of floating point numbers, then that difference can be ignored. That means those numbers are considered approximately equal.
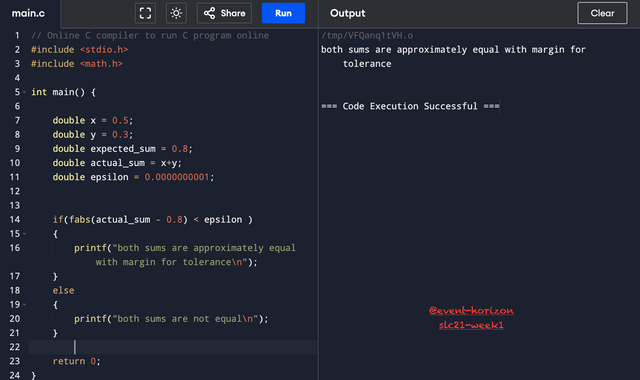
I have used the fabs function from the math library to compute the absolute value of the actual_sum, to discard the negative sign, if any.
Below is a classic example of PI which I have fixed with precision. I have considered values upto two decimal places by using .2f and avoided the rest to minimize the error as much as I can. How many decimal places should be considered depends on the scope of the program, sometimes even slightest of errors can't be overlooked so more decimal places are considered in computation.
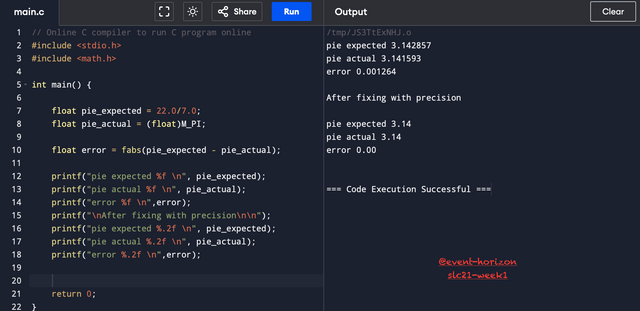
Please ignore the spelling of PI in the code. I was hungry.
Task # 4
1-Based on the example of counting digits in a number, write a program that determines:
(one of your choice):
The sum of the digits of a number, (3456 => 3+4+5+6=18), sum(3456) = 18

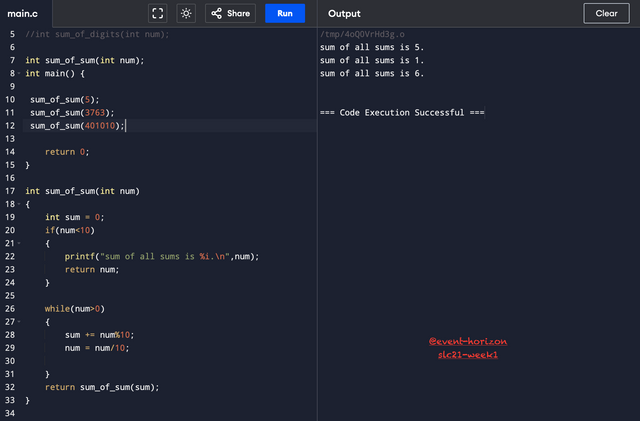
A modulus with 10 of any number gives its last digit, and division by 10 gives all the digits except the last. Using this simple logic, I computed all the digits and added them.
2-the sum of the digits of a number, but finding it for the sum, and for the sum of the sum, until you get a one-digit sum - (3456 => 3+4+5+6=18 => 1+8=9). Here you can do it directly as stated in the task, it won't be the best option, but you can think and find a more efficient solution, which I always ask to find. sum1(3456)=9
Here I simply peformed the previously defined function again and again in a loop until one digit was left.

It looks fine but didn't sit well with me because Recursion was on my mind all the time when I read this problem. I don't know if it's been taught in the previous season as I wasn't following back then.
Recursion is a unique function which calls itself and solves the problem by dividing into sub-problems. It has two main parts - a base case and recursive case. A base case is kind of a condition under which the function terminates. In this case, our base case is one digit. Then there's a recursive case in which a sub-problem is solved and the result is passed as argument to the function itself. Here, in the while loop, the sum of all digits is calculated. Then the function is called again with the result as argument and everything starts all over again until it reaches the base case and prints the final result/sum.
3- find the number of a specified digit in a number count_d(143112, 1) = 3, count_d(143112, 5) = 0.
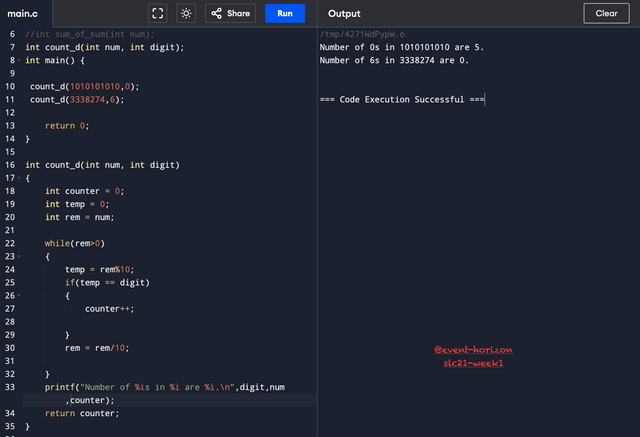
Here I have used the same logic of finding last digit through modulus with 10. When the digit found matches the number that needs to be counted then I set the counter for it. Then I divide the number with 10, get the same number except the last digit which is already checked. And repeat the process on it until all digits are checked.
Task # 5
As preparation for the next lesson and to review the past, find the largest of two numbers, then the largest of three numbers (this is a different subtask), then the largest of four, five, six, and seven-stop when you understand that you are not following a rational path and for larger quantities, you should do it differently. Complete the task only using the conditional operator if().
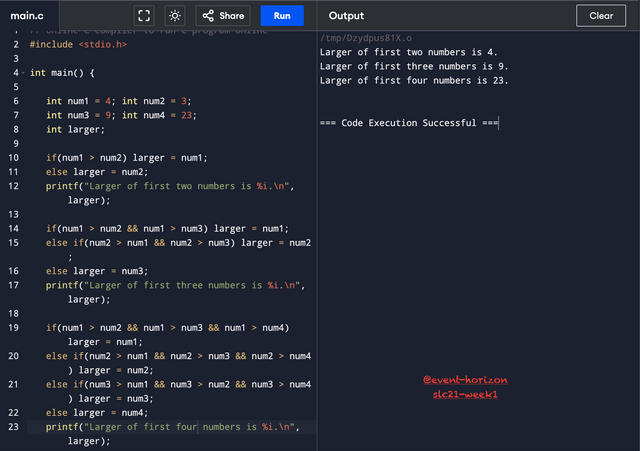
I got tired with only four numbers. It was getting chaotic. Need a better solution. :/
Task # 6
Perform the previous task using the ternary operator.
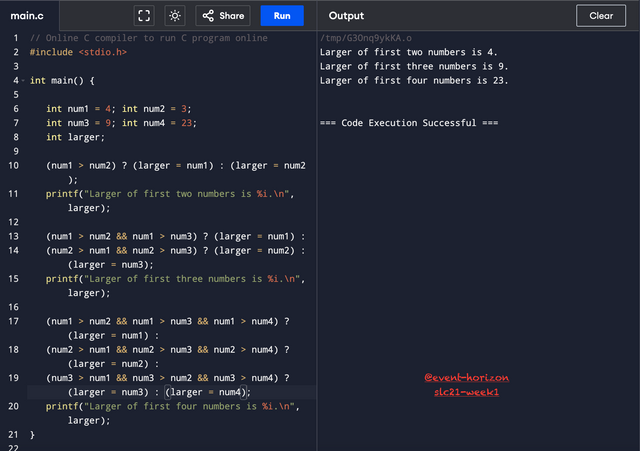
All the more chances for errors with an annoying number of ternary operators.
Task # 7
Perform the previous task by writing a function max() and using it.
Defining the function for finding the maximum value made things a bit easier. But these nested calls meant countless brackets - again more chance of syntax errors.
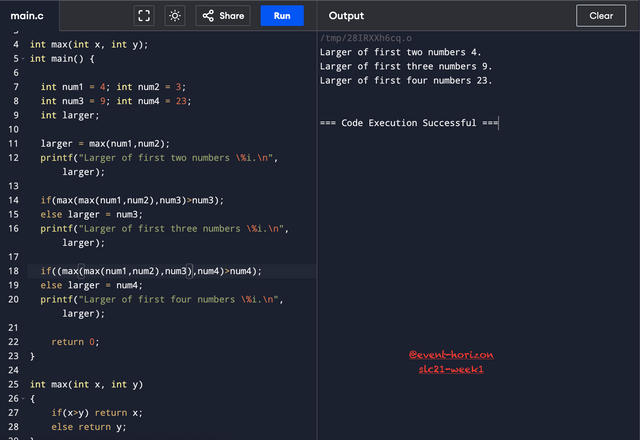
I used another approach, which is storing the previous larger number and feeding it directly to the max function instead of calling it again.
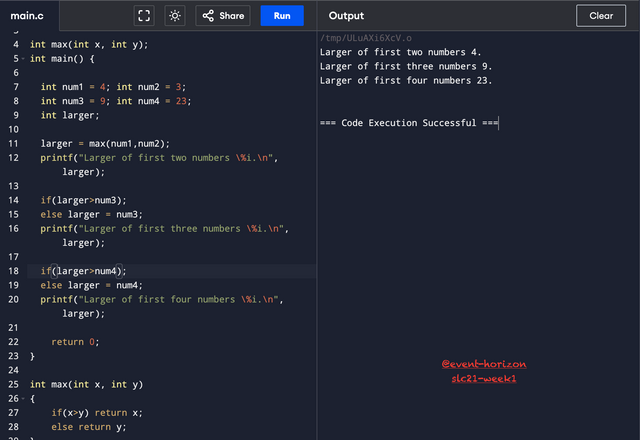
A more optimal way would be to write a recursive function that takes an array of numbers as one of the inputs.
Task # 8
Write functions:
1- that will print all the divisors of a given number print_div(number)—you can skip printing one and the number itself print_div(11) => (empty), print_div(12) => 2 3 4 6
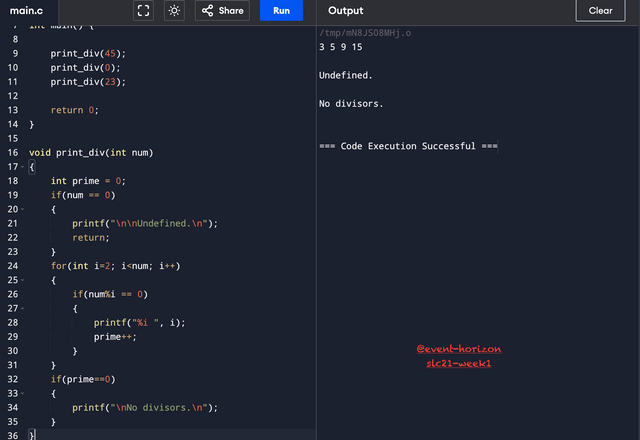
To find the divisors, I simply divided the input number by all numbers, starting from 2 to the number before the input number itself. As per the requirement, I skipped two divisors, number 1 and the number itself. I skipped zero as well to escape the program to crash or give a runtime error.
Since we are not supposed to use arrays and I'm simply printing the divisors, I have no record of how many divisors are printed. So, I created a variable prime and assigned it the value zero. I increased it by 1 every time a divisor is found. If there are no divisors found at the end the prime will stay zero, and the program will print, No divisors.
2- a function sum_div(number) that will calculate the sum of its divisors that are less than itself sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8,
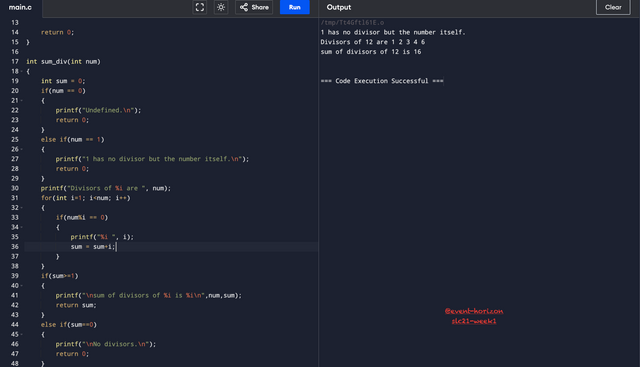
In print_div, 1 and the number itself is ignored but in sum_div 1 is considered. So, I have started the loop with 1 here. I have also written a separate condition for when the input number is 1.
Each divisor found is added to the variable sum which is initiated with zero. I didn't feel the need of prime here as in the previous code because if there are no divisors, sum would remain 0.
3- a function that will find and print perfect numbers from 1 to n (the number passed to the function) perfect numbers are those where the sum of divisors less than the number equals the number itself.
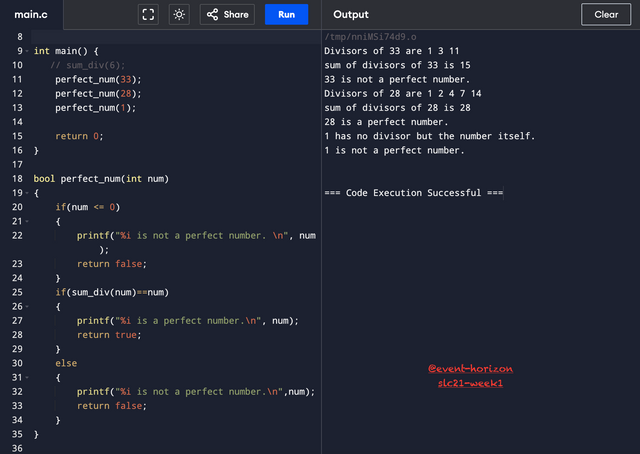
This one was simple because all the work is done in the previous code. I just had to check if sum_div was equal to input number. I had to add an additional check for 0 and negative integers because perfect numbers can only be positive integers.
Use of INLINE function
I wanted to demonstrate it in the task 7 but it turns out the compiler I'm using doesn't support it. I wrote max(x,y) function separately for clarity.
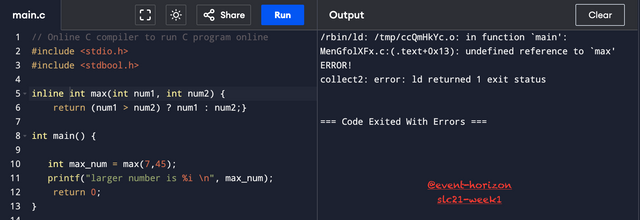
Interestingly, when I removed the keyword inline and let the rest of the syntax remain there, the function worked just fine.
All the screenshots are taken from the online compiler I used. The written code is solely my work. Cover image is also captured and edited by me.
That's a wrap. My eyes hurt now but I enjoyed problem solving and coding after ages. (:
Dabei würde ich gerne mal neben Dir sitzen und mir das erklären lassen um mal einen Eindruck von dieser Arbeit zu bekommen , ich lese öfter diese Post natürlich meist ohne zu verstehen was der Inhalt bedeutet , auch wenn sich das vielleicht Dumm anhört, bei mir ist das Blatt weis von Programmierungen habe ich Null Wissen , ich weis warum man Programme schreibt , aber nicht wie .
Und wegen dem Warum sage ich Danke für euere Arbeit 👍!
VgA
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for giving it a try even when you don't understand it and don't worry about being blank. I was in your shoes once.
I don't undersrand a word of German, bring your translator along, if you ever want me to explain this to you. (Assuming you don't understand English because I have never seen you writing anything except German.) 😀
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
We had many US soldiers in our area in the seventies and eighties, so I am more familiar with speaking than with reading and writing as far as US English is concerned
I would also have a trained translator (Chriddi) 😃
VgA
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit